№1. Из условия видим, что диагональ BD делит ромб на два правильные треугольника ABD и CBD. Можно по теоремме пифагора найти высоту этих треуг-ков, а затем их площадь, но для равностороннего треуг-ка есть такая формула площади:
S=(√3/4)*a^2
S=√3/4*10=2√3/5=0,7см^2
№2. Сторона правильного шестиугольника равна радиусу описанной около него окружности, поэтому r=6см.
Длина окр-ти l=2Пr=2*3,14*6=37,68см
S=Пr^2=3,14*36=113,04см^2
№3. Что-то не понял условие. Дан прямоугольный треугольник и найти радиус вписанного треугольника. Радиус вписанной окружности нужно найти.
r=S/p, где р-полупериметр. Так как острый угол 45, то катеты равны.
Пусть один катет равен х, тогда
x^2+x^2=100
2x^2=100
x^2=50
x=√50=5√2см
S=1/2*5√2*10=25√2см^2
p=(10+5√2+5√2)/2=5+5√2см
r=25√2/(5+5√2)=5√2/(1+√2)=2,93см
Вступление:
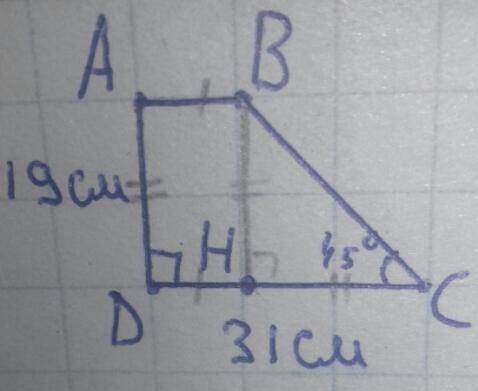
Пусть в прямоугольной трапеции ABCD, AB и CD основания, а ∠D прямой. Тогда AD меньшая боковая сторона (как расстояние между параллельными отрезками AB и CD), то есть AD=19см. По построению DC большое основание, поэтому по условию DC=31см. Острые углы при большом основании, ∠C=45° т.к. ∠D=90°.
H∈DC, BH⊥DC ⇒ BH=AD=19см.
В прямоугольном ΔBHC:
∠C=45°, ∠H=90° ⇒ ∠B=45°⇒ HC=BH=19см.
DH=DC-HC=31-19=12см.
В четырёхугольнике ABHD:
∠D=90°, ∠H=90° и ∠A=90°, ∠B=90° т.к. AB║DH, ведь H∈DC и AB║DC.
Получается ABHD - прямоугольник, поэтому AB=HD, HD=12см ⇒ AB=12см.
AB мень. осн. т.к. CD - большее.
Меньшее основание равно 12см.
1. элементарно, поскольку отношение неизвестного катета к гипотенузе рано 1/2, то есть углы 30 и 60 градусов (именно из вершины угла 60 градусов выходит биссектриса). Известный катет 6, поэтому остальные стороны 2*√3 и 4*√3.
2. пусть основание 2*х, боковые стороны 6*х.
Тогда косинус угла при основании равен х/(6*х) = 1/6;
по теореме косинусов из тр-ка, образованного медианой, половиной боковой стороны и основанием
(3*√11)^2 = (3*x)^2 + (2*x)^2 - 2*(2*x)*(3*x)*(1/6) = 11*x^2;
x = 3; основание 6;
3. плохое условие.
В треугольнике АМР известна площадь 21/2 и стороны РА = 3*√2 и АМ = 7;
поэтому синус угла МРА (обозначим его Ф) определен однозначно.
7*(3*√2)*sin(Ф) = 21/2; sin(Ф) = √2/2;
в условии сказано, что АМ- наименьшая из сторон, то есть угол Ф не может быть тупым, поэтому он равен 45 градусов, и его косинус положителен
cos(Ф) = √2/2;
но в этом случае получается
АМ^2 = 7^2 + (3*√2)^2 - 2*7*(3*√2)*(√2/2) = 25; АМ = 5, но это больше чем АР! то есть АМ - не наименьшая сторона. условие не верное.
но если заменить его на требование, что угол Ф острый, получается АМ = 5, МК = 10.
Может, я где ошибся, проверьте.