См рисунок во вложении
Последовательность действий такая:
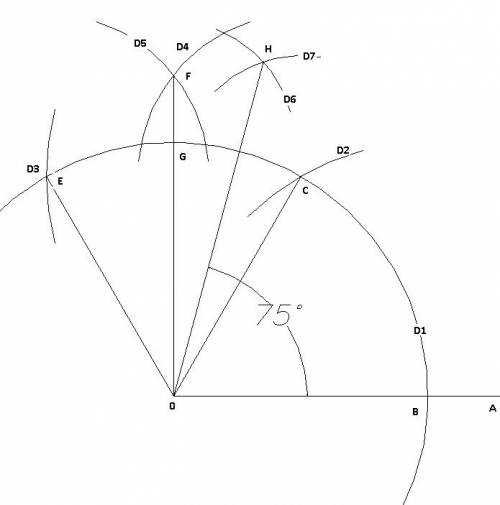
1. Проводим луч ОА
2. Из точки О строим дугу D1 радиусом R
3. На пересечении D1 и ОА ставим точку В.
4. Из точки В таким же радиусом R проводим дугу D2. На пересечении D2 и D1 ставим точку С.
5. Из точки С таким же радиусом R проводим дугу D3. На пересечении D3 и D1 ставим точку Е.
6. Из точки Е радиусом R1 проводим дугу D5, а из точки С таким же радиусом дугу D4. На пересечении ставим точку F.
7. Проводим отрезок ОF, на его пересечении с дугой D1 ставим точку G.
8. Из точки G радиусом R2 проводим дугу D6, из точки C радиусом тем же R2 проводим дугу D7, на пересечении D6 и D7 ставим точку Н. Угол НОВ=75 градусов.
Потому что угол ВОС=60, угол СОЕ=60, а G0C=30 и HOC=15
Трапеция прямоугольная. Если из вершины тупого угла трапеции (он такой один) опустить высоту, то вместе с диагональю эта высота разрежет трапецию на три равных равнобедренных прямоугольных треугольника. Кроме того, сама высота "отрезает" от трапеции квадрат со стороной, равной меньшему основанию и меньшей боковой стороне - она же высота.
Раз этот квадрат содержит 2 треугольника, а трепеция 3,
то площадь квадрата 18*2/3 = 12;
Получается, что меньшее основание и высота равны √12 = 2√3, а большее основание - в два раза больше, соответственно средняя линия - в полтора, то есть 3√3
(зачем было так числа подбирать, блин, нельзя было взять любой квадрат целого и умножить на полтора? например, площадь трапеции 24, высота и меньшее основание 4, большее 8, средняя линяя 6, проверка 6*4 = 24)
Если прямая, пересекающая одну из двух параллельных прямых находится в плоскости, определяемой этими параллельными прямыми, то она будет пересекать другую, т.к. по определению прямая бесконечна.
Если прямая, пересекающая одну из параллельных прямых находится под углом к плоскости (или перпендикулярна) определяемой параллельными прямыми, то пересекать другую она не будет.