а)в основании пирамиды прямоугольник. по теореме пифагора ас2=ad2+dc2=122+52=144+25=169ac=13.δ asc – равнобедренныйsa–ac=13перпендикуляр ah – высота равнобедренного треугольника, которая одновременно является и медианой.значит,sh=hcб)рассмотрим треугольник равнобедренный (sb=sc=13)треугольник sbc.высота sp равнобедренного треугольника делит сторону вс пополам.вр=рс=6в а) доказано, что sh=hc,значит hp – средняя линия δ sbc и hp|| sbпроводим pf ⊥ sb и hk || pf ⇒ hk ⊥ sb.hk=pfpf– высота прямоугольного треугольника sbp.sb=13bp=6sp=√sb2–bp2=√169–36=√133так как sδ sbp=(1/2)sb·pf и sδ sbp=(1/2)·bp·sp, тоpf· sb=bp·sb ⇒ pf=6·√133/13hk=pf=6·√133/13о т в е т.6·√133/13
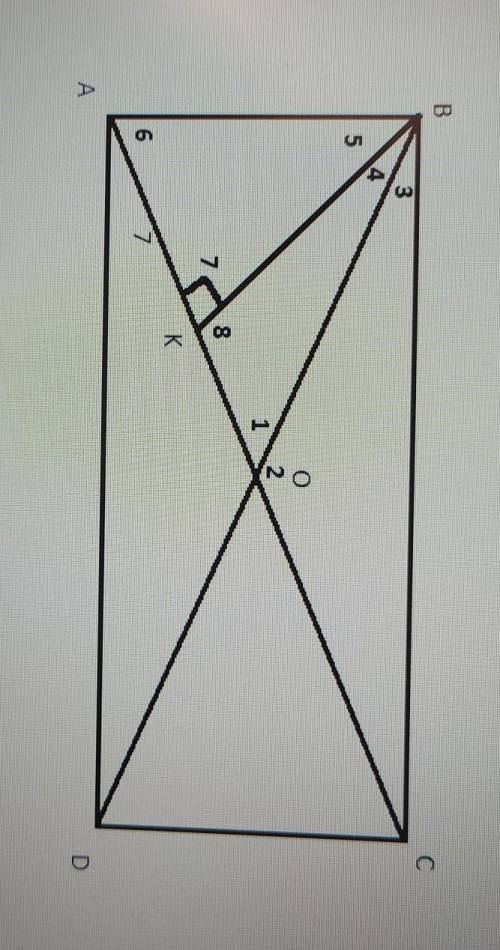
угол 1 = 60°, тогда смежный с ним угол 2 = 180° - 60° = 120°.
т.к. АВСД - прямоугольник, то ВО = ОС => треугольник ВОС - равнобедренный => угол 3 равен углу ОСВ = (180° - 120°) / 2 = 60° / 2 = 30°.
если ВК - перпендикуляр к АО, то угол ВКО = 90° => треугольник ВКО - прямоугольный => угол 4 = 90° - 60° = 30°.
т.к. угол АВС = 90° (АВСД - прямоугольник), угол 3 = 30°, угол 4 = 30°, то угол 5 = 90° - 30° - 30° = 30°.
если угол 5 = углу 4, АК - общая сторона и перпендикуляр, то треугольник АКВ = треугольнику ВКО => АК = КО = 7 (см) => АО = 7 + 7 = 14 (см).
Диагонали прямоугольника точкой пересечения делятся пополам => АС = АО · 2 = 14 · 2 = 28 (см)
всё:)