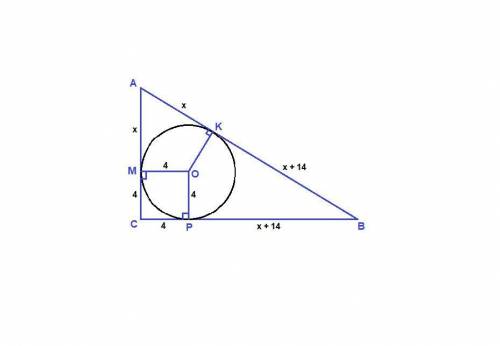
решение представлено на фото
Объяснение:


Радиус окружности, проведенный в точку касания, перпендикулярен касательной.
Значит ОК⊥АВ, ОМ⊥АС и ОР⊥ВС.
Отрезки касательных, проведенных из одной точки, равны. Обозначим один отрезок гипотенузы х, а другой х + 14. Тогда
АК = АМ = х
ВК = ВР = х + 14
СМОР - квадрат, СМ = СР = 4.
Составим уравнение по теореме Пифагора:
АВ² = АС² + ВС²
(x + (x + 14))² = (x + 4)² + (4 + x + 14)²
(2x + 14)² = (x + 4)² + (x + 18)²
4x² + 56x + 196 = x² + 8x + 16 + x² + 36x + 324
2x² + 12x - 144 = 0
x² + 6x - 72 = 0
x = 6 или х = - 12 - не подходит по смыслу задачи.
АС = 6 + 4 = 10 см
ВС = 4 + 6 + 14 = 24 см
Sabc = 1/2 AC · BC = 1/2 · 10 · 24 = 120 см²
Объяснение:
Дано:
Точка A:
Xa = 2;
Ya = -3.
Точка B:
Xв = -4;
Yв = 1.
Точка C:
Xc = -3;
Yc = -2.
Находим:
а)
Координаты вектора АВ:
AB = {Xв-Xa; Yв-Ya} = {-4-2; 1-(-3)} = { -6; 4}
б)
Координаты середины отрезка BC:
Xм = (Хв + Хс)/2 = (-4 -3)/2 = -7/2
Yм = (Yв + Yс)/2 = (1 - 2)/2 = -1/2
в) Расстояние между точками А и В
d = √ ( (-6)² + 4²) = √ (36+16) = √52 = 2*√13
2.
Чтобы найти координаты точки пересечения прямых, необходимо решить систему уравнений:
8x+6y=12
6x+3y=12
Умножим обе части второго уравнения на 2:
8x+6y=12
12x+6y=24
Вычтем из второго уравнения первое:
4х = 12
x = 3
y = -2