Пусть у нас есть квадрат ABCD
и прямоугольник EBFG. Вершины B прямоугольника и квадрата совпадают. Сразу оговоримся, что именование вершин фигур начинается с левого верхнего угла и продолжается по порядку по часовой стрелке.
Нам известно что AB = BC = CD = DA = 10 см., EB = FG = 3см., BF = GE = 4 см.
Тогда от сюда следует что новая фигура, образовавшаяся после выреза прямоугольника (AEGFCD) будет иметь следующие размеры:
AE = AB - EB = 10 - 3 = 7см.
EG = GE = 4 см.
GF = FG = 3 см.
FC = BC - BF = 10 - 4 = 6 см.
CD = 10 см.
DA = 10 см.
Ссумируем 7 + 4 + 3 + 6 + 10 + 10 = 40 см.
ответ 40 см.
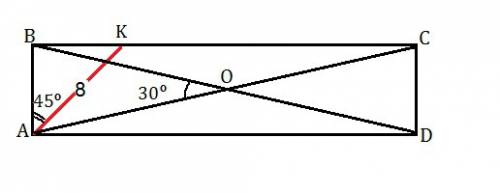
В прямоугольнике ABCD проведена биссектриса угла A до пересечения со стороной BC в точке K. Отрезок AK=8 см, угол между диагоналями прямоугольника равен 30°. Найдите стороны и площадь прямоугольника ABCD.
Обозначим точку пересечения диагоналей О.
Диагонали прямоугольника равны и точкой пересечения делятся пополам.
∆АОВ и ∆COD - равнобедренные, углы при АВ и CD равны по (180°-30°):2=75°⇒
в ∆ АВС ∠BСA=90°-75°=15°
∆ АВК - прямоугольный с острым углом ВАК=45°⇒
∠ВКА=45° ⇒ ∆ АВК равнобедренный.
АВ=АК*sin45°=(8*√2)/2=4√2 см
В ∆ АВС по т.синусов
АВ:sin15°=BC:sin75°
По таблице синусов
sin 15° =0,2588
sin75°=0,9659
4√2:0,2588=ВС:0,9659⇒
ВС=21,1127 см
S=AB•ВС=4√2•21,1127≈ 119,426 см²
------
Как вариант:
Найти из прямоугольного ∆ АВС диагональ АС:
АС=АВ:sin 15º=(4√2):0,2588
Площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними.
S=0,5•d₁•d₂•sinφ , где
d₁ и d₂ – диагонали, φ – любой из четырёх углов между ними/
Тогда S=0,5•{4√2):0,2588}²•0,5=≈ 119,426 см²
CB - x
AB - 20
x + 4 + x = 20
2x + 4 = 20
2x = 16
x = 8
AC = 8 + 4 = 12