Коэффициент подобия двух треугольников равен квадратному корню из отношения их площадей.
к=√(250/10)=5, ⇒ длина сходственной стороны - 3/5=0,6 см.
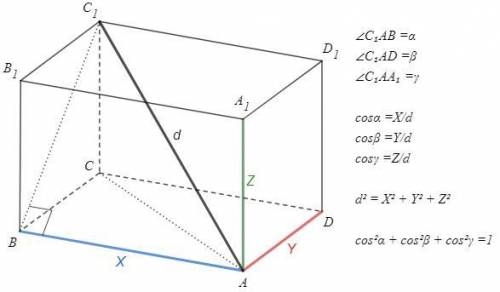
Прямоугольный параллелепипед
- ребра из одной вершины взаимно перпендикулярны
- противоположные грани - равные прямоугольники
AC1=d, AB=X, AD=Y, AA1=Z
AB⊥(BBC1) => AB⊥C1B
d^2 =Z^2 + AC^2 (т Пифагора)
AC^2 =X^2 +Y^2
=> d^2 =X^2 +Y^2 +Z^2
В прямоугольном параллелепипеде квадрат диагонали равен сумме квадратов трех измерений.
∠C1AB =a, ∠C1AD=b, C1AA1=y
cosa =X/d, cosb =Y/d, cosy =Z/d
Возведем в квадрат и сложим:
cosa^2 +cosb^2 +cosy^2 =(X^2 +Y^2 +Z^2)/d^2 =d^2/d^2 =1
Сумма квадратов направляющих косинусов вектора равна единице.
Через две параллельные прямые AA1 и BB1 проходит плоскость.
Плоскости AA1BB1 и p пересекаются по прямой A1B1.
Все общие точки двух плоскостей лежат на этой прямой.
Следовательно точка O лежит на прямой A1B1.
Диагонали трапеции AA1BB1 пересекаются в точке O.
S(BOA1) =S(B1OA) =5
(Это свойство трапеции. Треугольники BAA1 и B1AA1 имеют общее основание и равные высоты (расстояние между параллельными), следовательно их площади равны. Вычитаем общую площадь AOA1
=> S BOA1=S B1OA.)
Треугольники BOA1 и AOA1 имеют общую высоту, следовательно их площади относятся как основания, 1:2.
S(BOA1)/S(AOA1) =1/2 => S(AOA1) =5*2 =10
Аналогично
S(BOB1)/S(B1OA) =1/2 => S(BOB1) =5/2 =2,5
S(AA1BB1) =5 +5 +10 +2,5 =22,5

Для упрощения вычислений возьмем прямоугольный треугольник с меньшим катетом, равным 3 см и площадью 250 см².
Т.к. площадь треугольника равна половине произведения его высоты на основание, то второй катет в таком треугольнике равен 250·2÷3=500/3.
В подобном треугольнике с площадью 10 см² буду стороны, пропорциональные сторонам первого треугольника с коэффициентом пропорциональности k. Тогда получаем выражение
3k·500/3·k÷2=10
500k²=20
k=√0.04=0,2
Тогда сторона, сходственная стороне большего треугольника, равной 3 см, равна 3·k=3·0,2=0,6 см
ответ: 0,6 см