Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.
Объяснение:
Рисунок прилагается.
Дано: ABC прямоугольный треугольник, ∠ С = 90°, CH- высота, AH = 2 см - проекция катета AC на гипотенузу, BH = 18 см - проекция катета BC на гипотенузу.
Найти катеты AC и BC.
Обозначим для удобства катеты AC = a, BC = b, проекции катетов AH = a₁, BH = b₁, высоту CH = h.
Высота в прямоугольном треугольнике, опущенная на гипотенузу, равна среднему пропорциональному проекций катетов на гипотенузу.
h² = a₁*b₁ = 2 * 18 = 36; h = 6
⇒ Высота треугольника, опущенная на гипотенузу CH = h = 6 см.
Из прямоугольного ΔACH по теореме Пифагора:
a² = h² + a₁² = 6² + 2² = 36 + 4 = 40; a = √40 = 2√10
Катет AC = 2√10 см/
Из прямоугольного ΔBCH по теореме Пифагора:
b² = h² + b₁² = 6² + 18² = 36 + 324 = 360; b = √360 = 6√10
Катет BC = 6√10 см.
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.

Вариант решения.
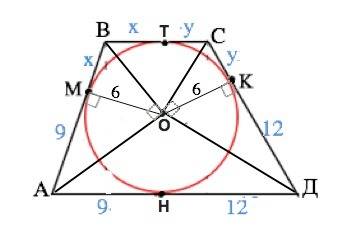
Обозначим трапецию АВСД, ВС и АД - основания.
Отрезки касательных к окружности, проведенных из одной точки, равны.⇒
АМ=АН=9, КД=ДН=12, ВМ=ВТ=х, СТ=СК=у
Соединим вершины трапеции с центром окружности.
Центр вписанной в угол окружности лежит на его биссектрисе.⇒ Центр вписанной в трапеции окружности лежит в точке пересечения биссектрис её углов.
Сумма углов при боковой стороне трапеции равна 180°, сумма их половин равна 90°, ⇒ ∆ АОВ и ∆ СОВ прямоугольные, радиусы ОМ и ОК– их высоты.
Высота прямоугольного треугольника - среднее пропорциональное между проекциями его катетов на гипотенузу.
ОМ²=АМ•ВМ
36=9•х⇒
х=36:9=4
Аналогично ОК²=ДК•СК
36=12•у
у=36:12=3
АВ=9+4=13
ВС=3+4=7
CD=12+3=15
АД=9+12=21
Площадь трапеции равна произведению высоты на полусумму оснований.
Высота описанной трапеции равна диаметру вписанной окружности
h=2r=12
S=(7+21)•12:2=168 ед. площади.
x^2+x^2=6^2
2x^2=36
x^2=18
x=v18=3v2
площадь боковой поверхности=Пи*3v2*6=18v2Пи
площадь полной поверхности=Пи*3v2*(3v2+6)=18Пи+18v2Пи