Найдите боковые стороны равнобедренный трапеции, основания которой равны 24 см и 18 см, а один из углов 120°

👇

Ответ:

sladkaiakailinn

27.07.2022

Назовём трапецию ABCD , угол ABC= углу BCD = 120, ведь трапеция равнобедренная.
Проведём высоту BK, угол ABK = 30 (угол ABC= 120, угол KBC=90, 120-90=30)
Проведём вторую высоту CM, угол DCM = углу ABK = 30
BC = KM = 18
AK = MD = 24-18 : 2 = 6:2 = 3
У нас есть прямоугольный треугольник ABK, AB - гипотенуза
Угол В 30 градусов, катет, лежащий против угла в 30 градусов равен половине гипотенузы, значит АВ = АК*2 = 3*2 = 6
АВ=СD = 6см

4,4(79 оценок)

Открыть все ответы

Ответ:

Амаpил1768

27.07.2022

Объяснение: квадрат диагонали параллелепипеда равен сумме квадратов его измерений:

Д²=дл²+шир²+выс²=

Д²=7²+6²+10²=49+36+100=185;

Д=√185см

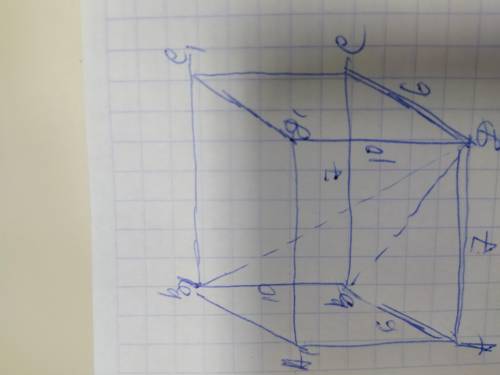
Если нужно найти диагонали граней параллелепипеда, тогда обозначим его вершины А В С Д В1 С1 Д1. Диагональ ВД делит грань АВСД на 2 равных прямоугольных треугольника, в которых стороны основания являются катетами а диагональ гипотенузой. Найдём диагональ ВД грани АВСД по теореме Пифагора: ВД²=АВ²+АД²=6²+7²=36+49=

=85; ВД=√85см. Такая же величина диагонали у грани А1В1С1Д1. Теперь найдём диагональ грани АА1ВВ1 также по теореме Пифагора:

АВ1²=АВ²+АА1²=6²+10²=36+100=136;

АВ1=√136=2√34см. Такая же величина диагонали у грани Д1ДС1С. Диагонали одной грани равны между собой.

Диагональ грани АА1ДД1=АД²+ДД1²=

=7²+10²=49+100=149; ДД1=√149см

Диагональ ДД1=√149см

Сторона основания прямоугольного параллелепипеда равна 6 см и 7 см, а высота 10 см. найдите диагонал

4,4(35 оценок)

Ответ:

Женя02458

27.07.2022

Дано6
Треугольник АВС- прямоугольный (угол В=90градусов), ВН - высота, АН=8, АВ=10
Найти: АС

Решение:
АС=АН+НС
1)Рассмотрим треугольник АВН, он прямоугольный, по определению высоты
$BH=\sqrt{AB^2-AH^2}=\sqrt{10^2-8^2}=\sqrt{100-64}=\sqrt{36}=6$
Катет противолежащий углы=равен произведению гипотенузы на синус этого угла, то есть
$BH=AB*sinBAC=\ \textgreater \ sinBAC=\frac{BH}{AB}=\frac{6}{10}=0,6$
Используя таблицу Брадиса найдем значение угла и получим, что угол ВАС=37 градусов
2) Рассматриваем треугольника АВС
угол АСВ=180-угол ВАС-угол СВА=180-37-90=53градуса
3)рассмотрим треугольник ВНС
Катет противолежащий углу равен произведению другого катета на тангенс этого угла, то есть
$BH=HC*tgC=\ \textgreater \ HC=\frac{BH}{tgC}=\frac{6}{tg53}=\frac{6}{1,3270}=4,5215=4,5$
4)AC=AH+HC=8+4,5=12,5
ответ: АС=12,5

Точка н является основанием высоты проведенной из вершины прямого угла в треугольника авс к гипотену