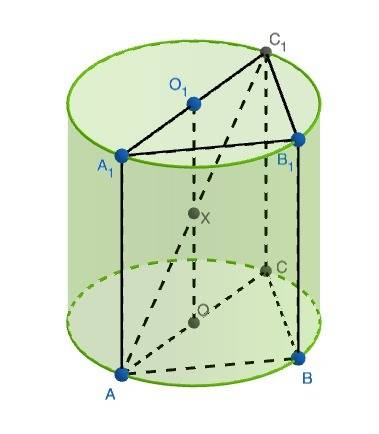
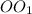 – ось цилиндра, проведем плоскость через прямые
– ось цилиндра, проведем плоскость через прямые 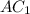 и
и 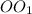 , обозначим точки A1 и C.
, обозначим точки A1 и C. 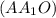 перпендикулярна основаниям, так как содержит
перпендикулярна основаниям, так как содержит 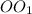 , поэтому
, поэтому 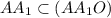 – образующая, перпендикулярная основаниям, тогда
– образующая, перпендикулярная основаниям, тогда 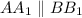 и
и 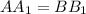 ,
, 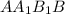 – прямоугольник, поэтому
– прямоугольник, поэтому 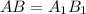 и
и 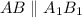 .
. 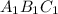 вписан в окружность верхнего основания и опирается на диаметр, значит, он прямоугольный и
вписан в окружность верхнего основания и опирается на диаметр, значит, он прямоугольный и 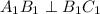 , а значит, и
, а значит, и 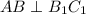 , поскольку
, поскольку 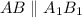 .
.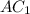 и
и 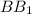 равен
равен 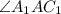 , т.к.
, т.к. 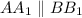 .
. 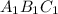 . В нем
. В нем 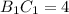 ,
, 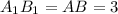 , тогда по теореме Пифагора
, тогда по теореме Пифагора 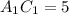 .
.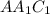
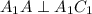 (
(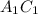 лежит в основании,
лежит в основании, 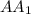 перпендикулярно основанию),
перпендикулярно основанию), 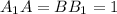 , тогда
, тогда 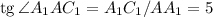 ;
; 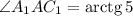 .
.