Pabcd = 34 дм.
Объяснение:
В равнобокой трапеции боковые стороны и углы при основаниях равны.
Пусть трапеция АВСD, ∠А = 60° - дано (так как острым может быть только угол при большем основании). Опустим высоты ВН и СР на основание AD.
Тогда в прямоугольном треугольнике АВН ∠АВН = 30° (по сумме острых углов прямоугольного треугольника), против угла 30° лежит катет, равный половине гипотенузы. АН = 5 дм.
Так как трапеция равнобокая, PD = AH = 5 дм.
Тогда ВС = AD - 2·АН = 12 - 2·5 = 2 дм.
Периметр данной трапеции равен
АВ+ВС+СD+AD = 2·10 +2 +12 = 34 дм.

38см
Объяснение:
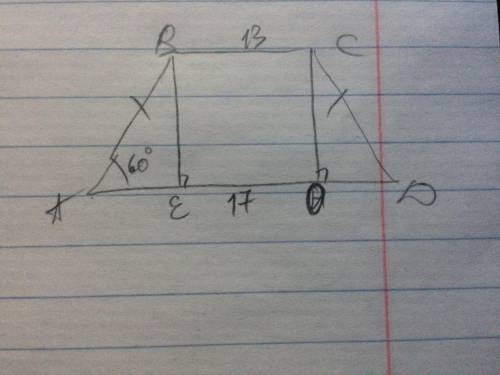
1. достроим высоты ВЕ и СО, тогда ВСОЕ - прямоуг(тк стороны попарно параллельны), следовательно ЕО=ВС=13см;
2. треуг АЕВ=треуг ДОС, по второму признаку равенства треугольников (УСУ):
угА=угД (тк трапеция равнобед);
АВ=СД (тк трапеция равнобед);
уг АВЕ=180-90-60=30 градусов=угДСО;
3. следовательно АЕ=ОД=(АД-ЕО):2=2см
4. рассм треуг АЕВ - прямоуг, тк ВЕ перпенд АД
уг АВЕ=180-90-60=30 градусов
АЕ = половине гипотенузы АВ , как катет против угла 30 градусов,
значит АВ = 2АЕ=2*2=4см
5. Р трапеции = 4+13+4+17=38см
Если что-то непонятно , пишите в комментах.
Успехов в учёбе! justDavid
1. Если АВ - диаметр, то координаты центра - это координаты середины отрезка АВ, которые равны полусуммам соответствующих координат начала и конца отрезка. В нашем случае: Xo=(Xa+Xb)/2 или Xo=(2+(-6)/2 = -2. Yo=(-4+8)/2 = 2.
ответ: координаты центра О окружности О(-2;2).
2. Радиус окружности с центром О(0;0) и проходящей через точку М(12;-5) равен модулю (длине) вектора (отрезка). Найдем его по формуле:
|OM| = √((Xm-Xo)²+(Ym-Yo)²) или |OM| = √((12-0)²+(-5-0)²) = √(144+25) = 13.
ответ: R = |OM| = 13.