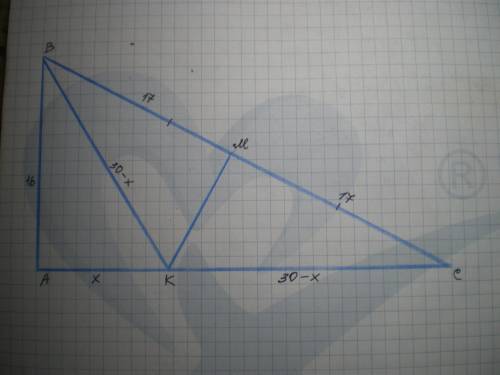
Дано: ΔАВС - прямокутний, ∠А=90°, АС=30 см, ВС=34 см; МК⊥ВС, ВМ=МС. Знайти МК.
Знайдемо АВ за теоремою Піфагора:
АВ=√(ВС²-АС²)=√(1156-900)=√256=16 см.
Проведемо ВК і розглянемо ΔВКС - рівнобедрений, тому що ВМ=СМ і МК⊥ВС, отже ВК=КС.
Нехай АК=х см, тоді КС=ВК=30-х см.
Знайдемо АК з ΔАВК - прямокутного:
АВ²=ВК²-АК²; 16² = (30-х)² - х²; 256=900-60х+х²-х²;
60х=900-256=644; х=10 11/15 см. АК=10 11/15 см, тоді
ВК = 30 - 10 11/15 = 19 4/15 = 289/15 см.
Знайдемо МК за теоремою Піфагора з ΔВМК, де ВМ=34:2=17 см.
МК²=ВК²-ВМ²=(289/15)² - 17² = (83521/225) - 289 = 18496/225.
МК=√(18496/225)=136/15=9 1\15 см.
Відповідь: 9 1/15 см.
Проведем диагональ AC.
S= S(ABCD) = S(ABC) +S(ADC) =(1/2)absinB + (1/2)cdsinD=
(1/2)absinB + (1/2)cdsin(180° -∠B)=(1/2)absinB + (1/2)cdsin∠B=(1/2)(ab + cd)sin∠B.
* * * ∠D +∠B =180° , sin∠D =sin(180° -∠B) =sin∠B ; cos∠D = - cos∠B * * *
Из треугольника ABC по теореме косинусов :
AC² =a² +b² -2abcos∠B . (1)
Аналогично из треугольника ADC :
AC²= c²+d² -2cdcos∠D ;
AC²=c²+d² +2cdcos∠B . (2)
Из уравнений (1) и (2) получаем :
a² +b² -2abcos∠B = c²+d² +2cdcos∠B ⇒ cos∠B = (a²+b² -c² -d²)/2(ab+cd) .
sin²∠B =1- cos²∠B =1- ((a²+b² -c² -d²)/2(ab+cd))² =
(1- (a²+b² -c² -d²)/2(ab+cd))(1+ (a²+b² -c² -d²)/2(ab+cd))=
((c+d)² -(a-b)²)/2(ab+cd))((a+b)² -(c-d)²)/2(ab+cd)) =
(c+d +b-a)(c+d +a-b)(a+b+d -c) (a+b+c -d)/ (2(ab+cd))² = || p = (a+b+c+d)/2|| =
(2p -2a)(2p -2b)(2p-2c)(2p-2d) / (2(ab+cd))² =4(p -a)(p -b)(p-c)(p-d) / (ab+cd)² .
sin∠B =2√((p -a)(p -b)(p-c)(p-d)) / (ab+cd) .
следовательно :
S =(1/2)(ab + cd)sin∠B =(1/2)(ab + cd)*2√((p -a)(p -b)(p-c)(p-d)) / (ab+cd) =
√((p -a)(p -b)(p-c)(p-d)).
2. Если указанный четырёхугольник ABCD можно описать около окружности ,то :
b+d= a+c (сумма противоположных сторон описанного четырехугольника равны).
p-c = (a+b+c+d)/2 - c =a+c -c =a ; * * * замена b+d = a+c * * *
p-d = (a+b+c+d)/2 - d =b+d -d=b ; * * * замена a+c=b+d * * *
p-a = (a+b+c+d)/2 - a =a+c -a =c ; * * * замена b+d = a+c * * *
p-b = (a+b+c+d)/2 - b =b+d -b=d . * * * замена a+c=b+d * * *
S =√(abcd) .