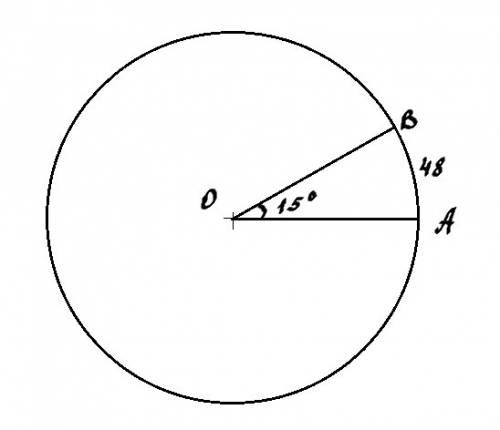
Угол АОВ центральный (смотри рисунок). Его градусная мера равна градусной мере дуги, на которую он опирается.
Малая дуга АВ равна 15°. Длина же ее равна 48.
Решим задачу, используя отношение.
Во сколько раз градусная мера большой дуги АВ больше градусной меры малой дуги АВ, во столько же раз длина большой дуги АВ больше длины малой дуги АВ.
Градусная мера всей окружности 360°.
360°–15° = 345° – градусная мера большой дуги АВ.
345°:15° = 23.
В 23 раза градусная мера большой дуги АВ больше градусной меры малой дуги АВ.
48*23 = 1104 – длина большой дуги АВ.
ответ: 1104.
1.
Да,т.к. сумма углов этого 4-угольника равняется 360 градусам
2.
по формуле (n-2)*180 найдем сумму углов (8-2)*180=6*180=1080 градусов
один угол равняется 1080/n=1080/8=135 градусов
3.
d=n*(n-3)/2=9*(9-3)/2=9*6/2=27
ответ:27 диагоналей
4.
P=48 см
Пусть одна сторона x ,тогда другая x-4
Составим уравнение x+x+x-4+x-4=48
4x-8=48
4x=48+8
4x=56
x=14
ответ:14см
5.
Сумма углов параллелограмма прилежащих к одной стороне равняется 180 градусам,пусть один угол 2x,тогда другой угол 3x,составим уравнение
2x+3x=180
5x=180
x=36
тогда углы параллелограмма 2*36=72 и 3*36=108
ответ:72,108,72,108.
6.
∠BCO=∠OCD,т.к. диагональ AC делит ∠BCD по полам
Треугольник OCD прямоугольный,тогда ∠OCD=180-(90+63)=180-153=27
ответ:27 градусов
Объяснение:
ВД=√10-биссектриса, АВ/ВС=АД/ДС=6/3=АД/ДС, 2/1=2х/х, АД=2х, ДС=х, АС=2х+х=3х, проводим высоту ВН на АС, площадь треугольника АВД=1/2*ВН*АД=1/2*2х*ВН=х*ВН, площадь ДВС=1/2*ДС*ВН=х*ВН/2, площадь АВС=1/2*АС*ВН=3х/2 * ВН, из отношения площадей находим площадь ДВС=1/3 площадиАВС, площадь АВД=2/3 площади АВС,
СМ-медиана, АМ=ВМ=3, медиана делит треугольник АВС на два равновеликих треугольника площадь АМС=площадь МВС=1/2площади АВС, треугольник МВК равнобедренный, ВМ=ВС=3,, ВО-биссектриса=медиана=высота, площадь МВО=площадьВОС=1/2площадь МВС=1/4площадьАВС,
площадь АМОД=площадьАВС - (площадьДВС+площадьМВС)=1-(1/3+1/4)=5/12 площадей АВС,
ВД=(1/АВ+ВС)*(корень(АВ*ВС*(АВ+ВС+АС)*(АВ+ВС-АС)=(1/9) * (корень18*(6+3+3х)*(6+3-3х))=(1/9)*(корень(18*(81-9х²), обе части в квадрат, 10*81=18*(81-9х²), х²=4, х=2=ДС, АД=2*2=4, АС=2+4=6
треугольник АВС равнобедренный, АВ=АС=6, проводим высотуВК на ВС=медиане=биссектрисе, ВК=КС=1/2ВС=3/2=1,5=3/2, треугольник АВК прямоугольный АК²=АВ²-ВК²=36-9/4=135/4, АК=(3√15)/2, площадь АВС=1/2*ВК*АК=1/2*3/2*(3√15)/2=(9√15)/4,
площадь АМОД=(5/12)*(9√15)/4=15√15/16