Две окружности касаются внешним образом. Их радиусы относятся как 3:1, а длина их общей внешней касательной равна 6√3.
Найдите периметр фигуры, образованной внешними касательными и внешними частями окружностей.
––––––––––––––
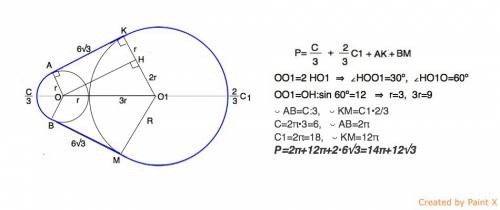
Обозначим O и O1 центры окружностей радиусов r и 3r соответствено.
Пусть AК и ВМ – общие внешняя касательные этих окружностей (точки A и В лежат на меньшей окружности, К и М– на большей). Соединим точки касания и радиусы соответственных окружностей.
Из О проведем перпендикуляр ОН к КО1.
АКНО – прямоугольник.
В ⊿ ОНО1 катет ОН=АК=6√3; катет НО1=2r, гипотенуза ОО1=r+3r=4r
Катет О1Н рпвен половине гипотенузы ОО1, следовательно,
∠ НОО1=30º, ∠ НО1=60º, и длина ОО1=ОН:sin 60º
4r=ОО1=6√3):(√3/2)=12
r=12:4=3
О1К=3r=9
Искомый периметр - сумма: ◡АВ -меньшей окружности, ◡КМ - большей окружности и длин АК и ВМ двух общих касательных.
∠АОО1=О1ОВ=∠АОН+∠НОО1=90°+30°=120°
◡АВ содержит угол АОВ=120º и равна 1/3 длины С меньшей окружности
С=2πr=6π
◡АВ=2π
∠КО1М=2∠КО1О=120°
меньшая ◡КМ внутри фигуры=1/3 длины окружности, большая
◡КМ =2/3 длины С1 большей окружности
С1=2π•9=18p
◡КМ=12π
Периметр равен сумме найденных длин дуг и длин двух общих внешних касательных.
Р=2π+12π+2•6√3=14π+12√3
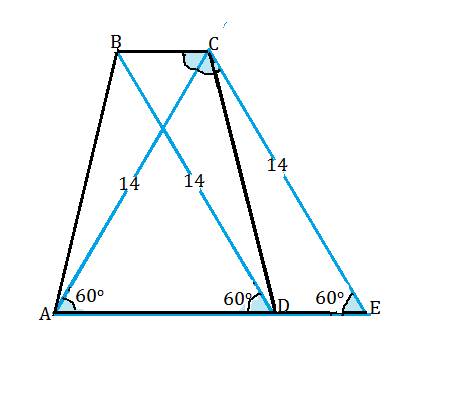
Диагонали равнобокой трапеции равны.
Из вершины С параллельно диагонали ВD проведем прямую до пересечения с продолжением АD в точке Е.
Углы САЕ и СЕА равны 60º (т.к. СЕ||ВD),
АС=ВD и ВD=СЕ по построению, ⇒
треугольник АСЕ - равносторонний, АЕ=14см.
ВС||АD, ВD||СЕ⇒ четырехугольник ВСЕD - параллелограмм, и DЕ=ВС. ⇒
АЕ=АD+ВС=сумме оснований трапеции.
Средняя линия трапеции равна полусумме оснований.
Средняя линия равна 14:2 =7 см