Пусть в треугольнике АВС угол С - прямой, АВ - гипотенуза, СМ - медиана к ней, CosА=3/5=0,6.
В прямоугольном треугольнике медиана проведённая к гипотенузе равна её половине.
АВ=2*СМ=2*10=20.
Длина катета АС относится к длине гипотенузы АВ как прилежащего угла CosА=0,6.
АС=АВ*СosA=20*0,6=12.
Второй катет ВС найдём по теореме Пифагора:
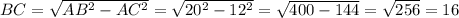 .
.
В прямоугольном треугольнике радиус вписанной окружности будет равен половине разности между суммой катетов и гипотенузой
r=(АС+ВС-АВ)/2=(12+16-20)/2=8/2=4.
ответ: радиус вписанной окружности равен 4.
1) Осевое сечение - прямоугольник, одна сторона 8см, а вторая равна диаметру, т.е. 6*2=12. Диагональ находим по теореме Пифагора √(144+64)=√208=4√13см
2) Диаметр d=√49=7, радиус r=3,5см Площадь основания S=Пr^2=3,14*12,25=38,5см^2
3) В основании круг радиуса 4см. S=Пr^2=3,14*16=50,24см^2
4) Площадь осевого сечения равна диаметру, умноженному на высоту S=d*h=8*4=32
5) S=d^2, d=2r=2*7,5=15, S=15^2=225
6) Площадь равна длине окружности, умноженной на высоту S=2Пrh, r=8/2=4, S=2*3,14*4*8=200,96.