Если из внешней точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью.
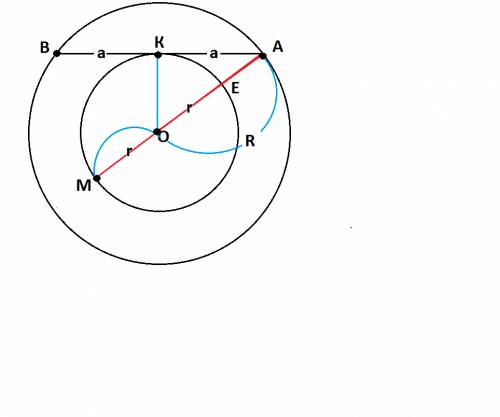
Для меньшей окружности точка А на большей окружности является внешней точкой.
АК²=АЕ*АМ
АЕ=R-r
AM=R+r
Пусть АК=а.
Тогда а²=(R-r)(R+r)=(R² -r²)
Т=π(R² -r²)⇒
Т=π*а²⇒
а=√(Т/π)
АВ=1а=2√(Т/π)
2)Медиана в равнобедренном треугольнике является и высотой, и медианой, и биссектрисой. Высота BM делит сторону AC пополам. Так как AC = AM+MC, AC=114, то AM=MC=114/2= 57.
3) По теореме Пифагора AB^2=AM^2+BM^2, отсюда BM=√(AB^2-AM^2) = √( 95^2-57^2)=√( 9025-3249)=√( 5776)= 76.
ответ: медиана ВМ=76.