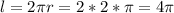(см. объяснение)
Объяснение:
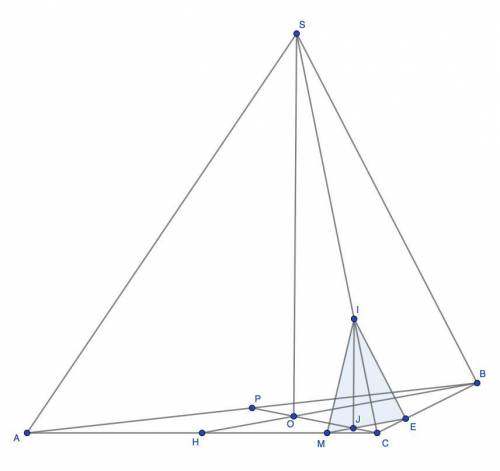
Поскольку пирамида правильная, то BH - медиана, биссектриса и высота треугольника ABC, то есть верно, что 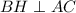 . Проведем прямую
. Проведем прямую 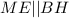 . Тогда
. Тогда 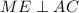 . Пусть CP другая медиана треугольника ABC. Пусть медианы этого треугольника пересекаются в точке O. Тогда из-за того, что пирамида правильная, SO - это ее высота, т.е.
. Пусть CP другая медиана треугольника ABC. Пусть медианы этого треугольника пересекаются в точке O. Тогда из-за того, что пирамида правильная, SO - это ее высота, т.е. 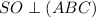 , а значит и любой прямой в этой плоскости. Пусть
, а значит и любой прямой в этой плоскости. Пусть  . Проведем через точку J прямую параллельную SO, которая пересечет SC в точке I. Тогда
. Проведем через точку J прямую параллельную SO, которая пересечет SC в точке I. Тогда 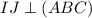 , а значит и любой прямой в этой плоскости. Соединим точки M, I и E. Получим плоскость
, а значит и любой прямой в этой плоскости. Соединим точки M, I и E. Получим плоскость 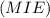 . Покажем, что
. Покажем, что 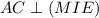 .
. 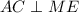 и
и 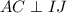 , и
, и 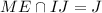 . Тогда задача сводится к нахождению площади треугольника
. Тогда задача сводится к нахождению площади треугольника 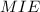 . Будем искать ее, как
. Будем искать ее, как 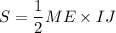 . Из подобия треугольников следует, что
. Из подобия треугольников следует, что 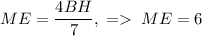 . Из подобия треугольников
. Из подобия треугольников 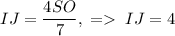 . Подставив найденное в формулу выше, получим
. Подставив найденное в формулу выше, получим 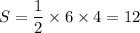 . Таким нами образом было получено, что искомая площадь равна
. Таким нами образом было получено, что искомая площадь равна 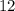 .
.
Задание выполнено!
4π
Объяснение:
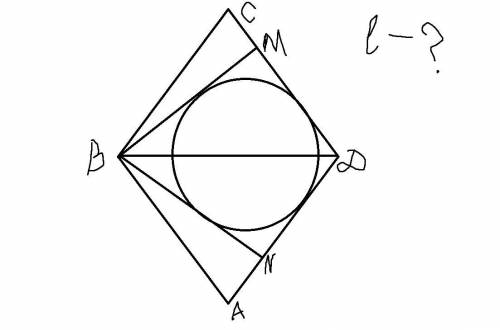
Как я понял, нам нужно найти длину окружности, вписанной в четырёхугольник BMDN. Я её изобразил на рисунке, хотя этого можно было и не делать. Обозначим длину этой окружности буквой l. Её нам нужно найти.
И давайте сразу из периметра найдём сторону ромба, она нам пригодится в решении. Обозначим для удобства сторону ромба буквой а. а=30/4=7,5.
Во-первых, проведём диагональ BD, которая разделяет угол В на два равных угла. Тогда ∠DBC = arctg2. Давайте теперь найдём косинус этого угла.
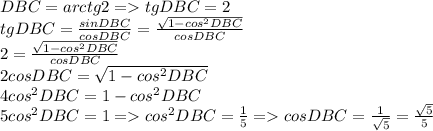
Тут может возникнуть вопрос по поводу знака косинуса. Да, косинус может быть отрицательным, но взгляните на наш ромб: угол, косинус которого мы искали, является острым. А если мы посмотрим на единичную окружность, то отрицательные косинусы могут быть лишь у углов 2 и 3 четвертей, т.е. это уже не острые углы. Значит мы берём именно такое положительное значение косинуса.
Треугольник BCD является равнобедренным, поэтому воспользуемся формулой для нахождения основания равнобедренного треугольника.
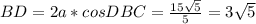
Вообще я сейчас пытаюсь найти высоту ромба, и чтобы её найти
нам ещё нужно найти синус угла В. Давайте найдём его:
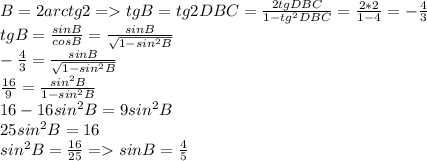
Теперь находим высоту ромба через синус тупого угла и меньшую диагональ:
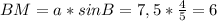
Из прямоугольного треугольника BMD найдём катет MD по теореме Пифагора:
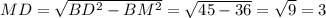
Давайте взглянем на треугольники BMD и NBD. Докажем их равенство. Эти треугольники будут равны, т.к. высоты ромба, проведённые из тупого угла равны, BD - общая для обоих треугольников, а диагональ ромба разделяет угол MBN пополам. Проще говоря, они равны по двум сторонам и углу между ними. Зачем нам это нужно? Это нужно для того, чтобы найти площадь и периметр четырёхугольника, в который вписана окружность. То есть, мы найдём площадь одного треугольника, умножим её на два, и получим площадь данного четырёхугольника. Также поступим и с периметром: найдём сумму катетов и умножим её на 2. Вообще для нахождения радиуса окружности нам нужен полупериметр, поэтому я периметр ещё поделю на 2. Ищем площадь и полупериметр четырёхугольника:
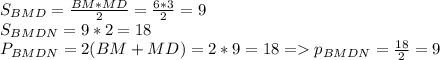
Теперь найдём радиус вписанной окружности по формуле:
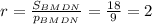
И теперь находиv длину окружности по формуле: