
Sполн = 16(12+√3)/3 см².
Объяснение:
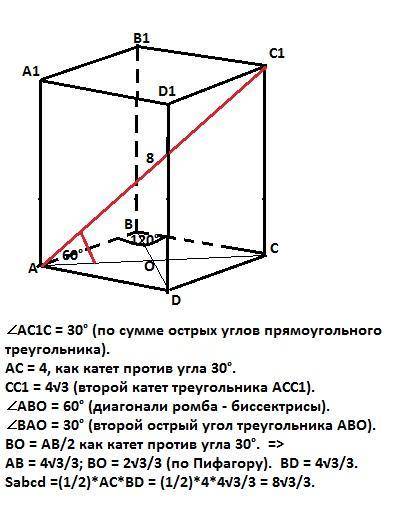
∠АС1С = 30° (по сумме острых углов прямоугольного треугольника).
АС = 4см (катет против угла 30°).
СС1 = 4√3см (второй катет треугольника АС1С).
∠АВО = 60° (диагонали ромба - биссектрисы).
∠АВО = 30° ( второй острый угол - диагонали ромба взаимно перпендикулярны).
ВО = АВ/2 как катет против угла 30°.
АВ = 4√3/3 см; ВО = 2√3/3см (по Пифагору). BD = 4√3/3см.
Sabcd = (1/2)·AC·BD = (1/2)·4·4√3/3 = 8√3/3см².
Sграни = АВ·СС1 = 4√3/3·4√3 = 16см².
S = 2·Sabcd+4·Sграни = 16√3/3 +4·16 = 16(12+√3)/3 см².
Объяснение:
Задача 1
а₃=15 см
Р=3*5=15(см),
S( прав.тр.)=(а²√3)/4 , S( прав.тр.)=(15²√3)/4 =(225√3)/4 (см²)
a₃ = R√3 , 15=R√3 , R=15/√3=5√3 (см)
r=R*( cos (180/n) ) , r=( 5√3 ) *( cos60 )=5√3 * (1/2)=2,5√3 (см) .
Задача 2
а₄=24 мм
Р=4*24=96 (мм)
S=а² , S=24²=576 (мм²)
r=1/2*а₄ , r=1/2*24 , r=12(мм)
R=r/( cos (180/n) ) , R=12/( cos45 ) =12:(√2/2)=24√2 (мм).
Задача 3
а₆=26м
Р=6*26=156 (м);
аₙ=2R*sin (180/n) , 26=2R*sin30 , 26=2R*(1/2) , R=26 м;
r=R*( cos (180/n) ), r=26* cos30 =26*(√3/2)=13√3 (м);
S=0,5Рr , S=0,5*156*13√3=1014√3 (м²)