Площадь круга находится по формуле s=pi*r^2, значит 9pi=pi*r^2, r^2=9, r=3
Если радиус круга равен 3, то диаметр 2r=3*2=6
Если провести в параллелограмме высоту из тупого угла, то эта высота будет равна величине диаметра и равна 6.
Так как сумма углов прилежащих к одной стороне параллелограмма равна 180 градусов, то острый угол равен 180-135=45.
Раз мы провели высоту, значит этот треугольник будет прямоугольным. А так как в прямоугольном треугольнике сумма острых углов равна 90 градусов, то значит другой острый угол равен 90-45=45. Его острые углы равны, значит этот треугольник равнобедренный и значит, раз он прямоугольный, его катеты равны 6.
По теореме пифагора находим гипотенузу. она равна 6 корням из 2(она же является одной из сторон параллелограмма).
Так как есть свойство, по которому если в многоугольник вписан круг, то суммы его противолежащих сторон равны. в параллелограмме(ABCD) это пары параллельных сторон(AB+CD=BC+AD).
Так как противолежащие стороны у параллелограмма равны, то: 2*6 корней из 2 = 2*x
x= 6 корней из 2
Это значит, что наш параллелограмм является ромбом, а значит его периметр равен: 4* 6 корней из 2 =24 корня из 2
ОТВЕТ: периметр параллелограмма равен 24 корня из 2
S=a*b
Площадь прямоугольника равна произведению смежных сторон.
Док-во:
Дано: ABCD - прямоугольник;
а и b - стороны прямоугольника.\
Док-ать, что S=ab
Докозательство:
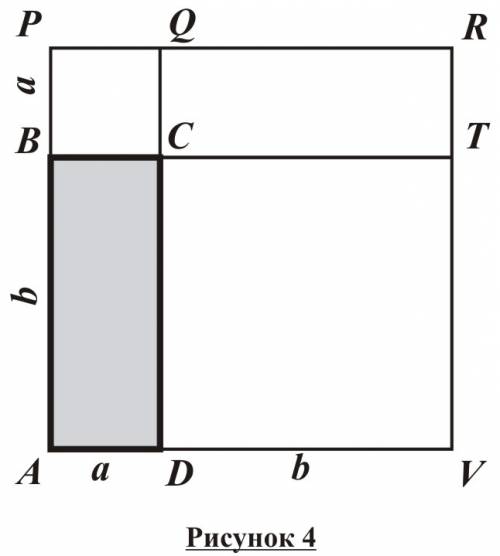
Достраиваем прямоугольник до квадрата сос тороной a+b
Т.к. площадь квадрата = квадрату его стороны,то площадь всего квадрата = (a+b)в квадрате.
С другой стороны,этот квадрат составлен из данного прямоугольника с площадью S,равного ему прямоугольника с площадью S (так как по свойству площадей,равные многоугольники имеют равные площади) и двух квадратов с площадями а^2 и b^2. Так как четырехугольник составлен из нескольких четырехугольников , то , по свойству площадей,его площадь равнв сумме площадей этих четырехугольников:
(а+b)^2=S+S+a^2+b^2 или a^2+2ab+b^2=2S+a^2+b^2
получаем: S=ab
Теорема доказана.
Площадь прямоугольника равна произведению его сторон (рис. 13.2.1):
S = a · b .
ДоказательствоПусть ABCD и AB 1 C 1 D – два прямоугольника с общим основанием AD (рис. 13.2.1).
Рисунок 13.2.1. Рисунок 13.2.2.Пусть S и – их площади. Докажем, что Разобьем сторону AB прямоугольника на некоторое число n равных частей, каждая из которых равна Пусть m – число точек деления, которые лежат нa стороне AB 1. Тогда Отсюда, разделив на AB , получим
(*)
Проведем через точки деления прямые, параллельные основанию AD . Они разобьют прямоугольник ABCD на n равных прямоугольников. Каждый из них имеет площадь Прямоугольник содержит первые m прямоугольника, считая от стороны AD , и содержится в m + 1 прямоугольниках. Поэтому Отсюда (**)
Сравнивая неравенства (*) и (**), заключаем, что При этом и – фиксированные числа, а n может быть выбрано сколь угодно большим. Следовательно, неравенство возможно только при Возьмем теперь единичный квадрат, прямоугольник со сторонами 1, a и прямоугольник со сторонами a , b (рис. 13.2.2). Площадь прямоугольника со сторонами 1 и a обозначим Сравнивая их площади, по доказанному будем иметь и Перемножая эти равенства почленно, получим S = a · b . Теорема доказана.