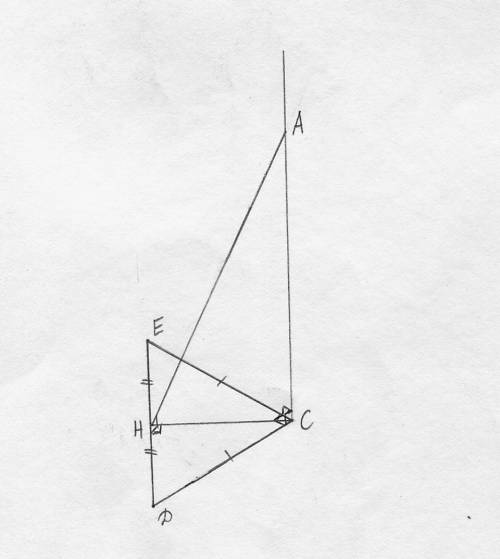
Две параллельные прямые пересечены секущей. Один из восьми образовавшихся углов равен 129 градусам. Найдите остальные углы.
Пусть ∠1 = 129°
∠1 + ∠2 = 180° (сумма смежных углов)
Тогда:
∠2 = 180 - ∠1 = 180 - 129 = 51°
∠2 = ∠6 = 51° (как соответственные при параллельных прямых)
∠6 = ∠3 = 51° (как накрест лежащие при параллельных прямых)
∠3 = ∠7 = 51° (как соответственные при параллельных прямых)
∠1 = ∠5 = 129° (как соответственные при параллельных прямых)
∠5 = ∠4 = 129° (как накрест лежащие при параллельных прямых)
∠4 = ∠8 = 129° (как соответственные при параллельных прямых)
ответ: ∠1, ∠5, ∠4, ∠8 = 129°; ∠2, ∠3, ∠6, ∠7 = 51°
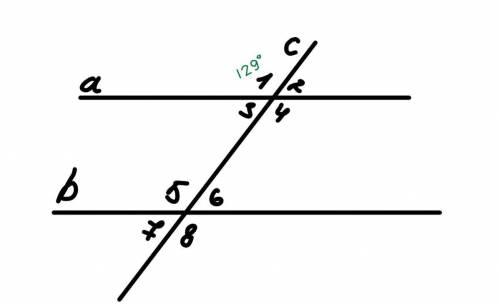
По теореме Пифагора:
BC^2=169-25=144
ВС=12
ответ: высота равна 12 дм.