Впрямоугольной трапеции боковые стороны 15 и 9 см ,а большее основание 20 см .найдите площадь трапеции

Question

Геометрия: Впрямоугольной трапеции боковые стороны 15 и 9 см ,а большее основание 20 см .найдите площадь трапеции

sirzikova · Accepted Answer

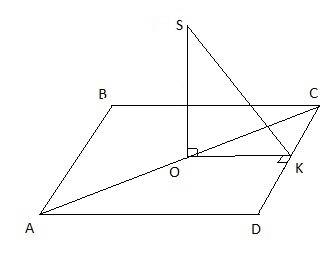
Из центра квадрата O проведем перпендикуляр OK к стороне CD.

Соединим точки S и K отрезком SK.

Т.к. по условию SO ⊥ ABCD, то SO ⊥ CD и OK является проекцией наклонной SK на плоскость ABCD. По построению OK ⊥ CD ⇒ по теореме о трех перпендикулярах SK ⊥ CD.

Следовательно ∠SKO будет двугранным углом при ребре CD и ∠SKO = 60°

Из прямоугольного ΔSKO:

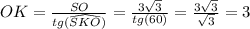
$OK=\frac{SO}{tg(\widehat{SKO})}=\frac{3\sqrt{3}}{tg(60)}=\frac{3\sqrt{3}}{\sqrt{3}}=3$

Найдем сторону квадрата. Т.к. точка O середина квадрата, то она является точкой пересечения диагоналей квадрата. Проведем диагональ AC и рассмотрим ΔACD.

OK ⊥ CD, AD ⊥ CD ⇒ OK ║ AD. Точка O - середина стороны AC ⇒ OK - средняя линия ΔACD.

AD = 2 * OK = 2 * 3 = 6

ответ: Сторона квадрата равна 6

Через центр о квадрата abcd проведен перпендикуляр os к плоскости квадрата. двугранный угол при ребр

MOGZ ответил