МК - ось симметрии, ⇒ все точки АВ и СD находятся от неё на равном расстоянии. ВМ=СМ=АК=DK.
а) Диагонали прямоугольника АС=ВD и точкой пересечения О делятся пополам ( свойство диагоналей прямоугольника).
Отрезки ВМ=АК, а РМ=РК по условию⇒ ∆ МВР = ∆ КАР по катету и гипотенузе. ВР=АР, а ∆ МРК - равнобедренный, МО=ОК. В ∆ АВС. отрезок РМ - средняя линия и параллелен диагонали АС. В ∆ АСD АК=КD, КТ║РМ по условию. Если одна из двух параллельных прямых параллельна третьей, то и вторая ей параллельна. ⇒ КТ║АС – средняя линия ∆ ADC. КТ=АС:2=РМ. Так как КТ - средняя линия ∆ АСD, то, точка Т - середина СD, из чего следует МТ - средняя линия ∆ ВСD. МТ и РК равны половине ВD, следовательно, равны между собой. Стороны четырехугольника КРМТ равны, следовательно, РМТК - ромб.
б) Вершины РМТК - середины сторон прямоугольника, его диагонали РТ и МК пересекаются под прямым углом и делят исходный прямоугольник на четыре равных меньшего размера. Диагонали этих меньших прямоугольников равны. ⇒ РК=АО=ОС, что и требовалось доказать.

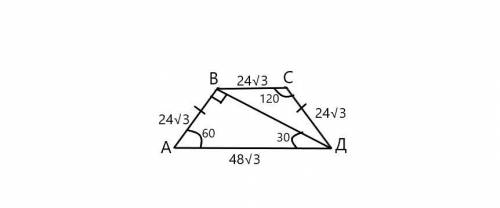
АВ=АД/2 (как катет лежащий против угла 30°) АВ=48√3/2=24√3; СД=АВ (трапеция равнобедренная); углы В и Д в треугольнике ВСД равны 30° (угол В в трапеции (180-60)=120°, угол В в треугольнике (120-90)=30°, угол Д в треугольнике (60-30)=30°); площадь трапеции равна сумме площадей треугольников АВД и ВСД; площадь треугольника равна половине произведения длин сторон на синус угла между ними.
S(АВД)=48√3*24√3*√3/4=864√3;
S(ВСД)=24√3*24√3*√3/4=432√3;
S(АВСД)=864√3+432√3=1296√3 ед².
Можно проще.
S(равнобедренной трапеции)=с*sinα(b-c*cosα), где b - основание , с - боковая сторона, α - угол при большем основании;
S=24√3*√3/2*(48√3-24√3/2)=36*36√3=1296√3 ед².
Еще можно через нахождение высоты, но думаю это лишнее.
Площади относятся как квадрат коэффициента подобия, периметры - как коэффициент подобия,
S2/S1=4 следовательно k^2=4 следовательно k=2, k - коэффициент подобия.
То есть P2=2P1, а P1+P2=48. Отсюда 3P1=48 и P1=16.