Рисунок во вложении.
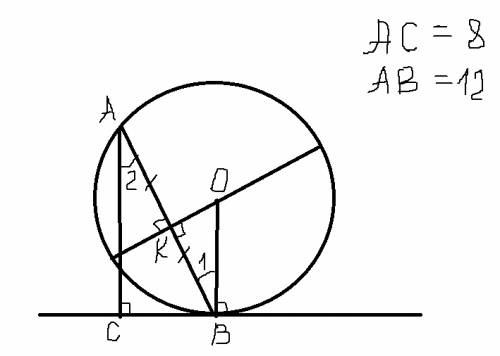
Назовем хорду АВ. Через точку В проведем касательную, из точки А проведем перепндикуляр АС к касательной-это и будет расстоянием от А до касательной. Получили прямоугольный треугольник АВС.
Теперь проведем диаметр окружности перпедикулярно хорде АВ. Он будет делить эту хорду пополам. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам. Точку пересечения хорды и диаметра назовем К .
Проведем радиус ОВ. Так как ОВ перпендикулярен касательной и АС перпендикулярен касательной, то ОВ//АС. Углы 1 и 2 накрест лежащие, значит они равны.
Рассмотрим треугольники АВС и ВОК: они прямоугольные и имеют по равному острому углу, значит они подобны. Из подобия следует, что ОВ:АВ=АС:ВК => ОВ:12=6:8 => ОВ=9
ответ: 9см.
Т.к. острый угол ромба 60 гр. то диагональ BD отсекает равыносторонний треугольник АВD все его стороны по а Т.к. параллельна ВА , то точка С находится на расстоянииа\2 от С до альфа. Двугранный угол АВ построим его линейный угол. Из D проведём перпендикуляр к АВ это DK Пусть проекция D на альфа будет точка Р Р это основание перпендикуляра. Соединим основание перпендикуляра и основание наклонной получим отрезок КР это проекция на альфа . По теореме о трёх перпендикулярах РК перпендикулярно альфа Тогда угол DKP это линейный угол двугранного угла ВА.sinDKP= DP\DK= а\2: а =1\2 значит угол 30 гр.
АЕ - биссектриса. ⇒ ∠ВАЕ=∠ЕАС=30°:2=15°. ⇒ ∠ВЕА=180°-120°-15°=45°
По т.синусов АВ/sin45°=BE/sin15°.
sin 45°=1/√2; sin 15°=(√3-1)/2√2 (по таблице)⇒ АВ√2=8•2√2/(√3-1) AB=16/(√3-1). Домножив числитель и знаменатель дроби на (√3+1), получим АВ=16(√3+1)/(√3-1)•(√3+1)=8(√3+1).
S(ABC)=AB•BC•sinABC/2 => S(ABC)=[8(√3+1)]²•√3/4=32√3( 2+√3) см²