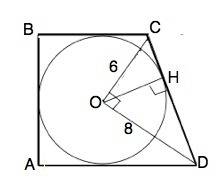
В трапеции АВСD. AD⊥AB⊥BC; О - центр вписанной окружности.
ОС=6, ОD=8. Найти площадь трапеции.
_______
Вписать окружность в четырехугольник можно тогда и только тогда, когда суммы его противоположных сторон равны.
Трапеция - четырехугольник.⇒
АD+BC=AB+CD
Центр вписанной в углы ВСD и СDA окружности лежит на пересечении их биссектрис. ⇒ ∠СОD=90°
По т.Пифагора CD=√(CO²+OD²)=10
Радиус ОН, проведенный в точку касания окружности и боковой стороны - высота ∆ СОD.
h=2S/CD
ОН=СО•OD:CD=6•8:10=4,8
АВ=2r=9,6=H
AD+BC=9,6+10=19,6
S=H•(AD+BC):2=94,08 (ед. площади)
1) Из формулы S=πR² выразим радиус:
R=√(S/π)=√(16π/π)=√16=4 см.
Т.к. осевое сечение - квадрат, следоватльно, высота цилиндра тоже равна R=h=4 см.
2) Полная площадь поверхности цилиндра находится по формуле:
S(полн)=2πRh+2S(осн)=2π*4*4+2*16π=32π+32π=64π см².
ответ: S(полн)=64π см².