Обозначения:
R — радиус описанной окружности;
r — радиус вписанной окружности;
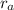— радиус вневписанной окружности, соответствующей стороне 
;
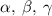— углы, противолежащие сторонам a, b и c соответственно;
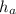— высота, соответствующая стороне a.
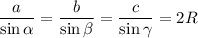— теорема синусов.
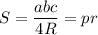— формулы площади треугольника.
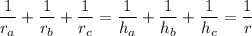— связь между радиусами вневписанных окружностей, длинами высот и радиусом вписанной окружности.
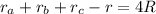
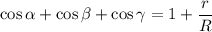
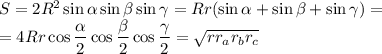
— менее известные формулы площади треугольника.
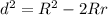— формула Эйлера, где d — расстояние между центрами вписанной и описанной окружностей.
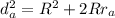— аналог формулы Эйлера для вычисления расстояния между центрами вневписанной (соответствующей стороне a) и описанной окружностей.
***
Этого хватит? Ведь записать «все» формулы невозможно: комбинируя имеющиеся формулы и находя новые зависимости, можно создать практически бесконечный список.
1).
Обозначим искомую сторону с
По теореме косинусов
с²=а²+b²- 2ab(cos(C)
с²=32+36 - 24√2·(135°)
Косинус тупого угла - величина отрицательная.
с²=32+36 - 24√2·(- 0.7071)
с²=68+ 24 · 0,999990=92
c=√92 см
c=2√23 см
-------------------------------
2).
ВД:(√2:2)=√6:(√3):2)
(√2:2)·√6= ВД·(√3):2)
√2 ·√6= ВД·√3
√12 = ВД·√3
2√3=ВД·√3
ВД=2
-----------------------------------
3).
Проведем ВН ⊥АД
ВН=НД как катеты равнобедренного ⊿ ВНД с углами при ВД=45°
ВД=ВН·√2
6√3 =ВН ·√2
ВН=6√3:√2
умножим числитель и знаменатель дроби 6√3:√2 на √2
ВН=6√3:√2=6√3·√2:√2·√2=3√6
sin BAH=ВН:АВ
sin BAH=3√6:6√2=√3·√2:2√2=√3:2
√3:2=sin (60°)
∠ВАД=60°
-----------
∠ВАД=∠ВСД=60°
∠АВС=∠СДА=120°