ответ: Р=36 см .
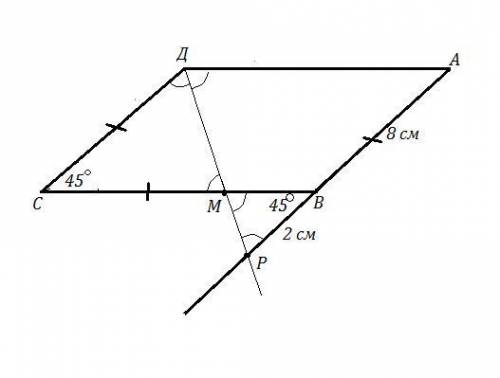
АВСД - параллелограмм , ДР - биссектриса, ∠С=45° ,
ДР пересекает АВ в точке Р , а ВС в точке М .
АР=10 см , ВР=2 см ⇒ АВ=10-2=8 см , СД=АВ=8 см как противоположные стороны параллелограмма .
ДР - биссектриса ⇒ ∠СДР=∠АДР .
∠АДР=∠СМД как накрест лежащие углы при АД || ВС и секущей ДР .
В ΔСМД два угла равны ⇒ ΔСМД - равнобедренный и СМ=СД=8 см ∠СМД=(180°-45°):2=67,5°
∠ВМР=∠СМД=67,5° как вертикальные .
В ΔВМР угол ∠МВР=45° , так как ∠МВР=∠МСД=45° как накрест лежащие углы при АР || СД и секущей ВС .
Но тогда в ΔВМР: ∠ВРМ=180°-45°-67,5°=67,5° , то есть ΔВМР есть два равных угла: ∠ВМР=∠ВРМ=67,5° , тогда этот треугольник равнобедрен-ный и ВМ=ВР=2 см .
Тогда ВС=СМ+ВМ=8 +2 =10 см , АД=ВС=10 см
Периметр Р=10+10+8+8=36 см .
.дано:ABCD-прямоугольник
АВ=5см
АС и ВD- диагоналипересекаютсяв точке О, под уг.60гр.
Рассмотрим образовавшейся треугольник АОВ
АО=ВО по свойству диагоналей в прямоугольнике следовательно треугольник АОВ равнобедреный
УголВАО=углуАВО т.к. труег.АОВ-равнобедренный, угол АОВ=60градусов следовательно Угол ВАО=углу АВО=(180-600):2=60 градусов по теореме о сумме углов треугольника
Т.к. углы в тругольнике равны, то треугольник АОВ равносторонний, следовательно АВ=Ао=ВО=5 см
Диагонали прямоугольника точкой пересечения делятся попалам, следовательно диагональ BD=5+5=10см