Пусть дан треугольник АВС, АВ=ВС. Он тупоугольный, т.к. АС²>АВ²+ВС²
ВВ1- высота к АС.
АА1=СС1 - высоты к равным боковым сторонам, и как высоты тупоугольного треугольника, проведенные к боковым сторонам, лежат вне его.
Высота равнобедренного треугольника, проведенная к основанию, является его биссектрисой и медианой. ⇒
АВ1=СВ1=30:2=15
∆ АВВ1=∆ СВВ1 ( по трем сторонам).
Из ∆ АВВ1 по т.Пифагора
ВВ1=√(AB²-AB1²)=√(17²-15²)=8 см
Высоты к боковым сторонам найдем из площади ∆ АВС
S=h•a:2
S(ABC)=BB1•AC:2=8•15=120 см²
h=2S:a=2S(ABC):BC
AA1=CC1=240:17=240/17=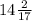 см
см

c=a^2+b^2-2abcos60
c^2=3^2+8^2-2*3*8*0.5=27+64-12=79
P=8+3+12=23