1) Четырехугольник ABCD — прямоугольник
Е, F, К и H— середины его сторон соответственно (точка Е на стороне АВ, точка А на стороне ВС, точка К на стороне CD, точка Н на стороне DA).
Четырехугольник EFKH — параллелограмм (так как ЕВ=СК и ВF=FC). Значит EF = FK, где EF и FK - стороны параллелограмма. Значит, EFKH — ромб.
2) Пусть четырехугольник ABCD является ромбом и Е, F, К, H — середины его сторон.
3) Четырехугольник EFKH — параллелограмм. Его стороны параллельны диагоналям ромба (как средние линии), а они перпендикулярны, значит, углы четырехугольника EFKH — прямые. Значит, четырехугольник EFKH — прямоугольник. Что и требовалось доказать.
Боковая сторона равна 4,15 см
Объяснение:
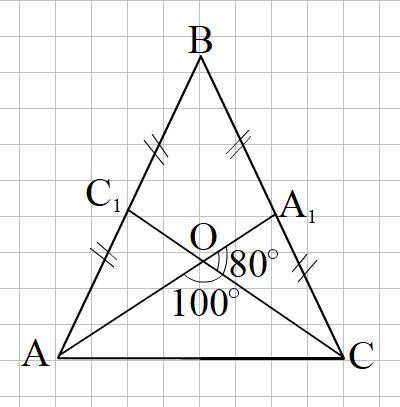
Смотри прикреплённый рисунок.
ΔАА₁В = ΔСС₁В по 1-му признаку равенства треугольников (АВ = ВС как боковые стороны равнобедренного треугольника, ВА₁ = ВС₁ как половинки равных боковых сторон треугольника и ∠В - общий угол)
Тогда медианы АА₁ = СС₁ = 3см
По свойству медиан треугольника АА₁ и СС₁ точкой пересечения О делятся в отношении 2 : 1, считая от вершины. Поэтому
А₁О = 1см, а ОС = 2см.
По свойству смежных углов ∠COА₁ = 180° - ∠АОС = 180° - 100° = 80°
В Δ СОА₁ по теореме косинусов можно найти половину боковой стороны СА₁
СА₁² = А₁О² + ОС² - 2 · А₁О · ОС · cos 80°
СА₁² = 1² + 2² - 2 · 1 · 2 · 0,1736 = 4,3054
СА₁ = √4,3054 = 2,075 (см)
ВС = 2 · СА₁ = 2 · 2,075 = 4,15 (см)
∠BCA=∠CAD- внутренние накрест лежащие при параллельных BC и AD и секущей AC
Треугольники BMC и DAM подобны по двум углам
По теореме Пифагора
АС²=10²+16²=100+256=356
АС=2√89
По теореме Пифагора
BD²=AB²+AD²=10²+24²=100+576=676
BD=26
Из подобия треугольников BMC и DAM следует пропорциональность сторон
BM: MD=BC:AD
BM:(26-BM)=16:24
16·(26-BM)=24BM
40BM=416
BM=10,4
MD=26-10,4=15,6
CM: MA=BC:AD
CM:(2√89 - CM)=16:24
16·(2√89 - CM)=24·CM
40·CM=32·√89
CM=0,4·√89
MA=√89 - 0,4·√89 = 0,6·√89
Р(Δ MAD)=MA+AD+DM=0,6√89+24+15,6=39,6+0,6·√89=0,6·(66+√89)=