Вот смотри....................

2) Находим уравнение плоскости α, проходящей через точку Р1(−4, 3, 5) и перпендикулярной заданной прямой L = Р1Р2:
(x + 4)/1 = (y − 3)/4 = (z − 5)/(−1).
Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n={A, B, C} представляется формулой:
A(x−x0)+B(y−y0)+C(z−z0) = 0. (2)
Направляющий вектор прямой L имеет следующий вид:
q = {m, p, l} = {1, 4, −1} (3)
Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (2) примет следующий вид:
m(x−x0)+p(y−y0)+l(z−z0) = 0 (4)
Подставляя координаты точки Р1 и направляющего вектора q в (4), получим:
1(x−(−4))+4(y−3)−1(z−5) = 0 (5)
Упростим уравнение (5): x+4 y−1 z−3 = 0. (6)
ответ. Уравнение плоскости, проходящей через точку Р1(−4, 3, 5) и перпендикулярной прямой (1) имеет вид x+4 y−1 z−3 = 0.
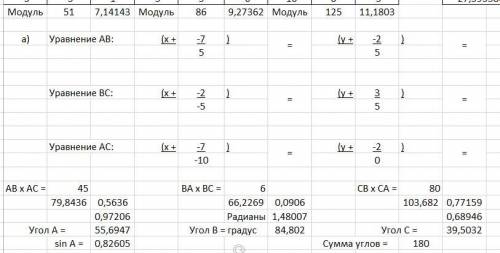
3) Дан треугольник ABC с вершинами A(7;2;3), B(2;-3;4), C(-3;2;-2).
Точка А Точка В Точка С
x y z x y z x y z
7 2 3 2 -3 4 -3 2 -2
Вектор АВ Вектор ВС Вектор АС
x y z x y z x y z
-5 -5 1 -5 5 -6 -10 0 -5
Модуль 51 7,14143 Модуль 86 9,27362 Модуль 125 11,18034
АВ х АС = 45 ВА х ВС = 6 СВ х СА = 80
79,8436 0,5636 66,22688 0,090598 103,6822 0,771588515
0,972056618 Радианы 1,480074279 0,689461756
Угол А = 55,69474166 Угол В = градус 84,80200957 Угол С = 39,50324876.
Данные расчёта в программе Excel плохо форматируются, поэтому дано фото во вложении.
А1 Если точка лежит в плоскости YOZ, то x=0;
ответ: а) A(0; 1; 1).
A2 Координаты середины отрезка равны полусумме координат концов отрезка:
x(М) = (x(A) + x(В))/2; ⇒ x(B)=2· x(M) - x(A);
x(B) = 2 · (- 2) - 1 = - 5
y(B) = 2 · 4 - 3 = 5
z(B) = 2 · 5 - (- 2) = 12
ответ: a) B(- 5; 5; 12).
A3 B(6; 3; 6) C(- 2; 5; 2)
Если АМ медиана, то M - середина ВС.
x(M) = (6 - 2)/2 = 2; y(M) = (3 + 5)/2 = 4; z(M) = (6 + 2)/2 = 4
M(2; 4; 4); A(1; 2; 3)
AM² = (2 - 1)² + (4 - 2)² + (4 - 3)² = 1 + 4 + 1 = 6;
AM = √6
ответ: а) √6
А4 Скалярное произведение равно сумме произведений соответствующих координат:
↑a · ↑b = 1 · (- 1) + (- 1) · 1 + 2 · 1 = - 1 - 1 + 2 = 0
ответ: б) 0.
А5 При симметрии относительно оси Ох меняют знак координаты у и z:
А(0; 1; 2) → A₁ (0; - 1; - 2),
B(3; - 1; 4) → B₁ (3; 1; - 4),
C(- 1; 0; - 2) → C₁ (- 1; 0; 2).
B1 Неполное условие. Должно быть так:
Диагональ осевого сечения цилиндра равна √81 см, а радиус основания – 3 см. Найти высоту цилиндра.
Осевое сечение цилиндра - прямоугольник, одна сторона которого (АВ) равна диаметру основания, а другая - образующая (она же высота).
Из прямоугольного треугольника АВВ₁ по теореме Пифагора:
ВВ₁ = √(АВ₁² - АВ²) = √(81 - 36) = √45 = 3√5 см
ответ: 3√5 см
B2 ΔSOA прямоугольный,
R = OA = SA · cos30° = 8 · cos30° = 8 √3/2 = 4√3 см
h = SO = SA · sin30° = 8 · 1/2 = 4 см
Sasb = 1/2 AB · SO = 1/2 · 2R · h = R · h = 4√3 · 4 = 16√3 см²
С1 Если призма вписана в шар, то ее основания вписаны в равные круги - параллельные сечения шара, а центр шара - точка О - лежит на середине отрезка КК₁, соединяющего центры этих кругов.
Отрезок, соединяющий центр шара с центром сечения, перпендикулярен сечению. ОК перпендикулярен плоскости АВС. Тогда КК₁ - высота призмы.
ОА - радиус шара, ОА = 4 см,
КА - радиус сечения, или радиус окружности, описанной около правильного треугольника АВС (призма правильная), тогда
КА = а√3/3, где а - ребро осноавния,
КА = 6√3/3 = 2√3 см
Из прямоугольного треугольника АОК по теореме Пифагора:
ОК = √(ОА² - КА²) = √(4² - (2√3)²) = √(16 - 12) = √4 = 2 см
КК₁ = 2ОК = 4 см
ответ: 4 см
Сумма двух сторон треугольника не может быть равна или меньше длины его третьей стороны.
Следовательно, третья сторона не может быть равна или больше суммы двух других, т.е. х ≨ 2,9
В то же время сумма третьей и одной из двух сторон не может быть меньше оставшейся стороны.
Пусть периметр треугольника
(0,8+2,1)+х=2,9+х
Тогда
0,8+х > 2,1
2,1+х > 2,9
До целого числа периметру треугольника недостает:
1).
0,1 м
Третья сторона не может быть такой длины.
Иначе сумма сторон 0,8+0,1=0,9, а оставшаяся сторона 2,1 больше, чем 0,9
2).
1,1 м
сумма сторон 0,8+1,1=1,9, а оставшаяся сторона 2,1 > 1,9
1,1- не подходит
3)
2,1
.. 0,8+2,1=2,9
Третья сторона этого треугольника может быть только 2,1 м.