площадь трапеции
площадь трапеции равна произведению полусуммы ее оснований на высоту:
s = ((ad + bc) / 2) · bh,
где высота трапеции — это перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание.
доказательство.

рассмотрим трапецию abcd с основаниями ad и bc, высотой bh и площадью s.
докажем, что s = ((ad + bc) / 2) · bh.
диагональ bd разделяет трапецию на два треугольника abd и bcd, поэтому s = sabd + sbcd. примем отрезки ad и bh за основание и высоту треугольника abd, а отрезки bcи dh1 за основание и высоту треугольника bcd. тогда
sabc = ad · bh / 2, sbcd = bc · dh1.
так как dh1 = bh, то sbcd = bc · bh / 2.
таким образом,
s = ad · bh / 2 + bc · bh = ((ad + bc) / 2) · bh.это можно только с доказательством
Объяснение:
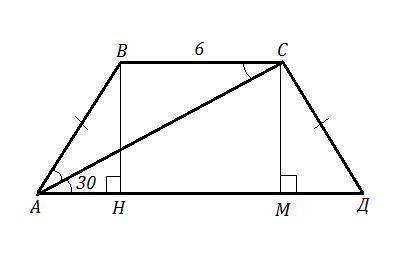
АВСД - равнобокая трапеция, АВ=СД, ВС=6 см, ∠АВС=120° , ∠САД=30°. Найти АС.
Так как ∠АВС=120°, то ∠ВАД=180°-120°=60° ,
∠САД=30° ⇒ ∠ВАС=∠ВАД-∠САД=60°-30°=30° .
Значит диагональ АС - биссектриса ∠А .
∠АСВ=∠САД=30° как внутренние накрест лежащие при АД || ВC и секущей АС ⇒ ΔАВС - равнобедренный , т.к. ∠ВАС=∠АСВ .
Значит, АВ=АС=6 см .
Опустим перпендикуляры на основание АД из вершин В и С: ВН⊥АС , СМ⊥АД , получим прямоугольник ВСМН и два треугольника АВН и СМД .
Рассмотрим ΔАВН: ∠ВНА=90°, ∠ВАН=∠ВАД=60° , АВ=6 см ⇒
∠АВН=90°-80°=30°
Против угла в 30° лежит катет, равный половине гипотенузы ⇒ АН=6:2=3 см.
Так как ΔАВН=ΔСМД (по гипотенузе АВ=СД и острому углу ∠ВАД=∠АДС), то МД=АН=3 см.
НМ=ВС=6 см как противоположные стороны прямоугольника ВСМН.
АД=АН+НМ+МД=3+6+3=12 см.