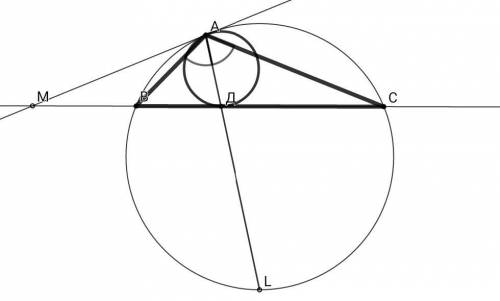
Докажем лемму Архимеда через дополнительное построение. Проведём к окружностям общую касательную АМ, пересекающая прямую ВС в точке М. Пусть ∠BAD = α, ∠CAD = β, ∠ACB = γ, тогда ∠ВАМ = ∠АСВ = γ (по свойству угла между касательной МА и хордой АВ), ∠MAD = γ + α, ∠ADB = ∠CAD + ∠ACD = β + γ (по свойству внешнего угла ΔACD). MA и MD - касательные к малой окружности ⇒ МА = MD - как отрезки касательных, ΔAMD - равнобедренный, ∠MAD = ∠MDA ⇒ γ + α = β + γ ⇒ α = β , AD - биссектриса ∠ВАС, ч.т.д. Конечно, данную лемму можно доказать в 2 строчки, заметив гомотетию окружностей, но это дело вкуса.
а и с-противоположные углы
обозначим угол с за х тогда угол а будет 4х тогда
4х+х=180
5х=180
х=36 угол с
4*36=144 угол а
144-58=86 угол в
180-86=94 угол д
если в трапецию вписана окружность то у неё сумма боковых сторон равна сумме оснований
сумма боковых сторон=сумме оснований=12*2=24
периметр=24*2=48