Уравнение окружности: x2+y2=72. Уравнение прямой: x+y+c=0. Найди значения коэффициента c, с которым прямая и окружность имеет одну общую точку (прямая касается окружности).
Объяснение:
x²+y²=72, x+y+c=0
у=-(х+с). Подставим в уравнение окружности .
x²+(-(х+с))²=72 , х²+х²+2сх+с²-72=0 , 2х²+2хс+(с²-72)=0. Это уравнение должно иметь одно решение ( прямая и окружность имеет одну общую точку ), значит Д=0
Д=(2с)²-4*2*(с²-72)=4с²-8с²+8*72=-4с²+8*72,
-4с²+8*72=0 , -4с²=8*72, с²=2*72, с²=144 , с=±12
ответ . -12; 12
Дано:
тр АВС (уг С=90)
АС = 16 см
ВС = 12 см
АВ = 20 см
Найти:
а) косинус меньшего угла
б) сумму квадратов косинусов острых углов
а) по свойству соотношения сторон и углов треугольника, против меньшей стороны лежит меньший угол, а значит меньшим будет угол, лежащий против стороны 12 см, по условию, следовательно, это угол А.
cos A = AC / AB; cos A = 4/5 = 0.8
б) Есть св-во - оно же основное геометрическое тождество, сумма квадратов косинусов острых углов прямоугольного треугольника равна единице, но вы похоже этого ещё не изучали, посему надо найти оставшийся косинус угла В и найти сумму квадратов косинусов вычислением, приступим:
cos B = CB / AB; cos B = 12/20 = 3/5 = 0.6
cos²A +cos²B = 0.8²+0.6²=0.64+0.36=1
Сделай лучшим решением
Если квадрат и ромб имеют одинаковые периметры, тто они имеют и одинаковые стороны. Воспользуемся следующей формулой для вычисления площади параллелограмма в случае ромба.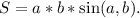
В данном случае стороны равны, значит формула упрощается до 
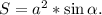. Заметим, что 
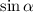Это угол между сторонами ромба. Здесь не имеет значения острый или тупой, так как в обоих случаях будет положительный ответ. Площадь квадрата же всегда равна 
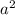. Заметим, что синус всегда меняется в данном случае от 0 до 1. То есть только в случае синуса равного 1 (а это квадрат) площадь ромба равна площади квадрата, в остальных случаях площадь ромба всегда меньше площади квадрата.