Любые две из трех прямых, соединяющих середины отрезков AB и CD; AC и BD; AD и BC могут быть:
а) параллельны одной из этих прямых.
Через две параллельные прямые можно провести плоскость, притом только одну.
б) пересекаться:
Через две пересекающиеся прямые можно провести плоскость, притом только одну.
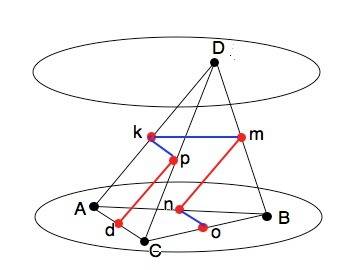
В рисунке приложения даны некоторые из получающихся пар параллельных и пересекающихся прямых:
а) pd и mn как средние линии треугольников АСD и BCD параллельны AD; kp и no параллельны основанию АС треугольников АDC и АВС.
б) km и mn, mn и no пересекаются.
Составить уравнение прямой , проходящей через точки А(2,-10) ,О(0;0).
Уравнение прямой проходящей через начало координат О(0;0) имеет вид у= к*х.
Тк А принадлежит данной прямой , то ее координаты удовлетворяют уравнению прямой -10=к*2 ⇒ к=-5. Уравнение прямой у=-5х
Общее уравнение прямой проходящей имеет вид у= к*х+b.
Тк O принадлежит данной прямой , то ее координаты удовлетворяют уравнению прямой 0==к*0+b ⇒b=0
Тк А принадлежит данной прямой , то ее координаты удовлетворяют уравнению прямой -10=к*2+0 ⇒ к=-5.
Уравнение прямой у=-5х
если 3000 см.куб - 10 см, то 5 см - 1500см.куб,
элементарно, Ватсон