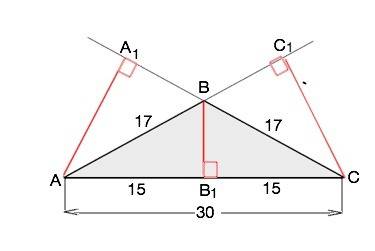
Назовём данный треугольник АВС.
ВВ1- высота к АС.
АА1=СС1 - высоты к равным боковым сторонам.
Высота равнобедренного треугольника, проведенная к основанию, является его биссектрисой и медианой. ⇒
АВ1=СВ1=30:2=15 см
∆ АВВ1=∆ СВВ1 ( по трем сторонам).
Из ∆ АВВ1 по т.Пифагора
ВВ1=√(AB²-AB1²)=√(17²-15²)=8 см
Высоты к боковым сторонам найдем из площади ∆ АВС
Заметим, что ∆ АВС - тупоугольный ( АС² > АВ²+ВС²), поэтому высоты, проведенные к боковым сторонам тупоугольного треугольника, лежат вне его.
S(ABC)=BB1•AC:2=8•15=120 см²
AA1=2S(ABC):BC
AA1=CC1=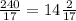 см
см
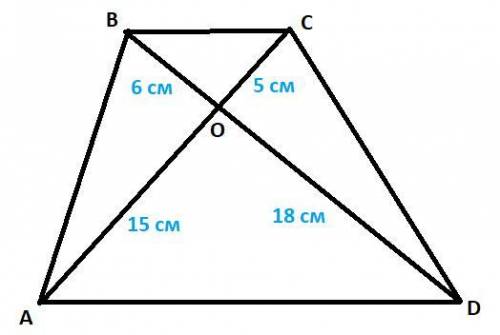
Условие: Диагонали четырехугольника ABCD AC и BD пересекаются в точке O так, что OC = 5 см, OB = 6 см, OA = 15 см, OD = 18 см. Докажите, что в четырехугольнике ABCD BC ║ AD и найдите отношение площадей треугольников AOD и BOC.
Дано: ABCD - четырехугольник, AC ∩ BD = O, OC = 5 см, OB = 6 см, OA = 15 см, OD = 18 см.
а) Доказать: BC ║ AD.
б) Найти: 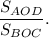
а) Доказательство:
ΔAOD подобен ΔBOC по двум пропорциональным сторонам и углу между ними:
OA/OC = 15/5 = 3/1 и OD/OB = 18/6 = 3/1 ⇒ OA/OC = OD/OB∠AOD = ∠BOC - как вертикальные углыЗначит, ∠ВСО = ∠DAO, а это равные накрест лежащие углы.
Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.
⇒ BC ║ AD, что и требовалось доказать.
б) Решение:
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
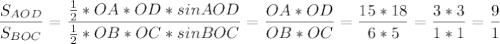
ответ: а) доказано ; б) 9 : 1.