ку) кр на 176 стр задание 5? :)
го хэлпану :
как мы знаем Sполная = Sбоковая + 2Sосновы.
у нас ABCD прямоугольник, мы с легкостью найдём его диагональ CA.
рассмотрим треугольник допустим ABC, мы знаем что у него угол B = 90 градусам так как он часть большого прямоугольника, и знаем две его стороны, допустим BC = 3см, а ВА = 6см. По теореме Пифагора найдём гипотенузу СА. СА=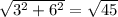
см.
теперь рассмотрим треугольник С1СА, он тоже прямоугольный, угол С=90 градусов. Нам известно сколько равно СА, и сколько равна диагональ С1А. По теореме Пифагора найдём высоту СС1. СС1=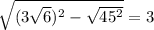 
см. Теперь мы знаем высоту СС1=Н.
Найдём Sбоковую. Sбок= Р(основы)*Н. Р = 3+3+6+6=18см => Sбок = 18*3= 54см^2. Теперь найдём Sосновы. Так как основание прямоугольник, то площадь будет равна произведению сторон Sосновы = 3*6= 18см^2.
и теперь наконец-то вернёмся к полной площади Sполная = 54+2*18= 90см^2.
С тебя лайк :)
Теорема 1. В треугольнике против большей стороны лежит больший угол.
Доказательство. Пусть в треугольнике ABC сторона АВ больше стороны АС (рис.1, а).
Рис.1
Докажем, что ∠ С > ∠ В. Отложим на стороне АВ отрезок AD, равный стороне АС (рис.1, б). Так как AD < АВ, то точка D лежит между точками А и В. Следовательно, угол 1 является частью угла С и, значит, ∠ C > ∠ 1. Угол 2 — внешний угол треугольника BDC, поэтому Z 2 > Z В. Углы 1 и 2 равны как углы при основании равнобедренного треугольника ADC. Таким образом, ∠ С > ∠ 1, ∠ 1 = ∠ 2, ∠ 2 > ∠ B. Отсюда следует, что ∠ С > ∠ В.
Справедлива и обратная теорема (ее доказательство проводится методом от противного).
Теорема 2. В треугольнике против большего угла лежит большая сторона.
Из теоремы 1 вытекает
Следствие 1. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
Доказательство следствия проводится методом от противного.
Из следствия 1 следует, что если три угла треугольника равны, то треугольник равносторонний.
Из теоремы 2 получаем
Следствие 3. В прямоугольном треугольнике гипотенуза больше катета.
С использованием теоремы 2 устанавливается следующая теорема.
Теорема 3. Каждая сторона треугольника меньше суммы двух других сторон.
Следствие 4. Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства:
АВ < АС + СВ, АС < АВ + ВС, ВС < ВА + АС.
