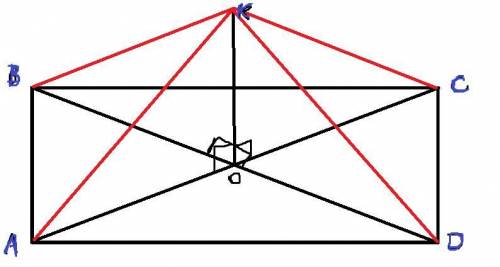
Точка O - центр пересечения диагоналей(+диагонали прямоугольника равны), значит OA=OB=OC=OD
Рассмотрим треугольник AKC:
1)AO=OC
2)OK-общая
3)Угол AOK= Угол COK
Из этого следует что треугольники AOK и COK равны.
Рассмотрим треугольник BKD:
1)BO=OD
2)OK-общая
3)Угол BOK= Угол DOK
Из этого следует что треугольник BOK и DOK равны.
Так же можно рассмотреть остальные две пары треугольников(AOK и BOK, COK и DOK) и сделать вывод что все угольники (AOK,BOK,COK,DOK) равны между собой, а значит гипотенузы у них всех равны, а значит точка K равноудалена от точек A,B,C,D.
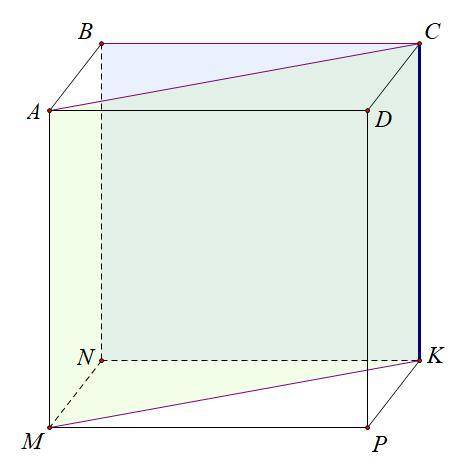
ответ: ∠NKM (или ∠BCA)
Объяснение:
1. CK ⊥ NK (CKNB -- квадрат), CK ⊥ KP (NKPM -- квадрат), NK ⊂ (NKP), KP ⊂ (NKP) ⇒ CK ⊥ (NKP) (по признаку перпендикулярности прямой плоскости)
2. Теорема 1 (признак ⊥ плоскостей): если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
CK ⊥ (NKP), CK ⊂ (ACK) ⇒ (NKP) ⊥ (ACK) (по теор. 1)
CK ⊥ (NKP), CK ⊂ (BCK) ⇒ (NKP) ⊥ (BCK) (по теор. 1)
3. Теорема 2: Если две плоскости перпендикулярны третьей, то линии их пересечений с третьей плоскостью образуют двугранный угол данных плоскостей.
(NKP) ⊥ (ACK), (NKP) ⊥ (BCK), (NKP) ∩ (ACK) = MK, (NKP) ∩ (BCK) = NK ⇒
⇒ ∠MKCB = ∠(ACK, BCK) = ∠(NK, MK) = ∠NKM (по теор. 2)
* задачу можно решить через верхнюю плоскость, тогда ответ: ∠BCA. Оба верные.
Допустим что углы 1 и 2 равны. Отложим от луча МN угол PMN,равный углу 2,так чтобы угол PMN и угол 2 были накрест лежащими углами при пересечениии прямых MP и В секущей MN.По построению эти накрест лежащие углы равны, потому MPIIB.Мы получили, что через точку М проходят две прямые (прямые А и MP),паралелельные прямой В. Но это противоречит аксиоме параллельных прямых. Значит наше допущение НЕВЕРНО и угол 1 = 2.