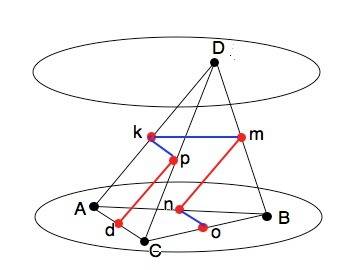
Любые две из трех прямых, соединяющих середины отрезков AB и CD; AC и BD; AD и BC могут быть:
а) параллельны одной из этих прямых.
Через две параллельные прямые можно провести плоскость, притом только одну.
б) пересекаться:
Через две пересекающиеся прямые можно провести плоскость, притом только одну.
В рисунке приложения даны некоторые из получающихся пар параллельных и пересекающихся прямых:
а) pd и mn как средние линии треугольников АСD и BCD параллельны AD; kp и no параллельны основанию АС треугольников АDC и АВС.
б) km и mn, mn и no пересекаются.
2 задача
угол BЕF=180 - угол AEF (смежные углы), следовательно равен углу А (условие задачи)
По первому признаку подобия треугольников треугольник EBF и треуг ABC подобны (угол В общий а два соответственных угла равны)
Площадь четырех уголника равна площади треугольника АВС - площадь треуг EBF
Такдже Sefca/Sebf=16/9
Sefca=16*Sebf/9
Sabc=16*Sebf/9 + Sebf (*9)
9*Sabc=16Sebf+9Sebf
9*Sabc=25Sebf (Отношение площадей треугольников)