Биссектриса делит угол пополам, т.е. ∠ABD = ∠DBC; ∠BAD=∠DAC.
1) \sf \angle \,BAD=\frac{1}{2}\angle\, A=\frac{1}{2}\cdot 50^\circ=25^\circ∠BAD=21∠A=21⋅50∘=25∘
\sf \angle\, ABD=\frac{1}{2}\angle \, B=\frac{1}{2}\cdot100^\circ=50^\circ∠ABD=21∠B=21⋅100∘=50∘
И рассмотрим треугольник ABD в нем сумма углов должна быть равна 180°,т.е. \sf \angle \,ADB=180^\circ-25^\circ-50^\circ=105^\circ∠ADB=180∘−25∘−50∘=105∘
2) Аналогично с примером 1)
\sf \angle \,BAD=\frac{1}{2}\angle\, A=\frac{1}{2}\cdot \alpha=\frac{\alpha}{2}∠BAD=21∠A=21⋅α=2α
\sf \angle\, ABD=\frac{1}{2}\angle \, B=\frac{1}{2}\cdot\beta=\frac{\beta}{2}∠ABD=21∠B=21⋅β=2β
\sf \angle \,ADB=180^\circ-\frac{\alpha}{2}-\frac{\beta}{2}=180^\circ-\frac{1}{2}(\alpha+\beta)∠ADB=180∘−2α−2β=180∘−21(α+β)
3) Сумма углов треугольника ABC равна 180°, т.е. ∠A+∠B+∠C=180°.
∠A + ∠B + 130° = 180°
∠A + ∠B = 180° - 130°
∠A + ∠B = 50°
∠ADB = 180° - 1/2(∠A + ∠B) = 180° - 1/2 * 50° = 180° - 25° = 155°
4) Аналогично с примером 3)
∠A + ∠B + ∠C = 180°
∠A + ∠B + \gammaγ = 180°
\sf \angle\, A+\angle \, B=180^\circ-\gamma∠A+∠B=180∘−γ
Тогда
\begin{gathered}\sf \angle\, ADB=180^\circ-\frac{1}{2}(\angle \, A+\angle \, B)=180^\circ-\frac{1}{2}(180^\circ-\gamma)=180^\circ-90^\circ+\frac{\gamma}{2}=\\ \\ =90^\circ+\frac{\gamma}{2}\end{gathered}∠ADB=180∘−21(∠A+∠B)=180∘−21(180∘−γ)=180∘−90∘+2γ==90∘+2γ
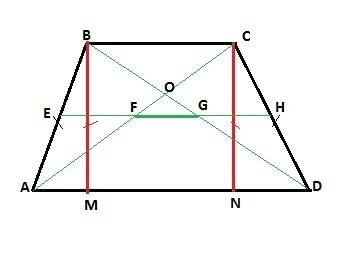
1. Пусть дана РАВНОБОКАЯ трапеция АВСD. Проведем ДВЕ высоты ВM и СN из вершин тупых углов. Образовавшиеся прямоугольные треугольники АВM и DCN равны по катету и гипотенузе. У равных треугольников против равных сторон лежат равные углы. Следовательно, <A = <D, что и требовалось доказать.
2. Соединим середины диагоналей АС и ВD отрезком FG и продлим его в обе стороны до пересечения с боковыми сторонами трапеции АВ и CD в точках Е и H соответственно. В равнобокой трапеции диагонали равны, следовательно, AF=DG и FO=GO (точка О - точка пересечения диагоналей). Тогда в треугольнике АОD отрезок FG параллелен основанию AD. => Прямая ЕН - средняя линия трапеции, а EF и GH - средние линии треугольников АВС и DBC. => EF=GH=BC/2. => EH=BC+FG.
Средняя линия ЕН трапеции равна полусумме ее оснований, то есть ЕН=(BC+AD)/2 => BC+AD=2EH => BC+AD =2(BC+FG). => FG=(AD-BC)/2, что и требовалось доказать.
Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон.
Пусть СМ=х
Тогда ВМ=4-х.
АС:АВ=СМ:МВ
3:5=х:(4-х)
5х=12-3х
8х=12
х=1,5
СМ=1,5 см
МВ=4-1,5=2,5 см
У треугольников АВМ и АМС разные основания, но высоты равны АС=3 см
S ⊿АСМ=АС·СМ:2=2,25 см²
S ᐃ АВМ=АС·ВМ:2=3,75 см²
Проверка:
S ⊿АВС=S ⊿АСМ+S ᐃ АВМ
S ⊿АВС=3·4:2=6 см²
S ⊿АСМ+S ᐃ АВМ=2,25+3,75=6 см²