66,66,48
Объяснение:
Внешний угол равен сумме двух углов несоседних с ним, тобишь сумме углов при основе. Поскольку треугольник у нас равнобедренный, то эти углы между собой равны и, чтобы найти каждый из них мы делим их сумму надвое
1) 132:2=66
Дальше просто за суммой углов треугольника находим третий угол.
2) 180-66-66=48
Или же мы можем найти третий угол другим тут сами выбирайте. Итак, угол при вершине и внешний угол смежные, то есть их сумма равна 180 градусов, поэтому просто:
2) 180-132=48
В принципе нет разницы как найдёте третий угол. Все равно что там по сути 180-132, что там) удачи
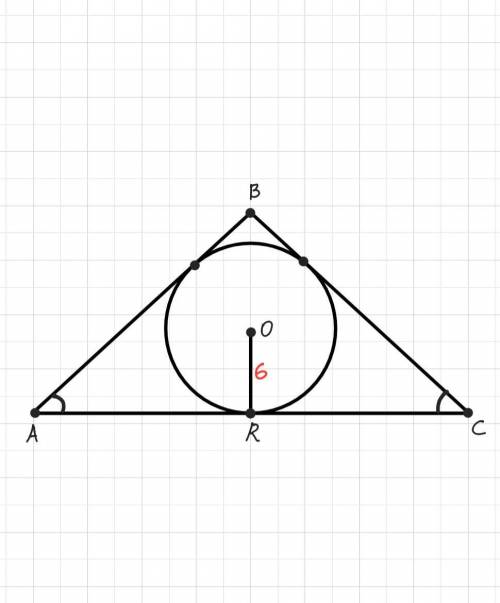
Дано: ΔABC - равнобедренный, АВ=ВС, Sabc= 192 см², АС=АВ+4, окружность, впис. в ΔАВС, OR - радиус, OR= 6 см
Найти: АВ, ВС, АС.
Решение.
Пусть АВ=ВС= х см. По условию основание на 4 см больше, чем боковая сторона, значит, АС= х+4.
Площадь треугольника равна произведению полупериметра треугольника на радиус вписанной окружности.
S= p•r, где S - площадь треугольника, p - его полупериметр, r - радиус вписанной окружности.
Находим периметр ΔАВС.
Р= АВ+ВС+АС= х+х+х+4= 3х+4.
Полупериметр равен соответственно р= (3х+4)/2.
S= p•r;
192= (3x+4)/2 •6;
192= (3х+4)•3;
192= 9х+12;
9х= 192–12;
9х= 180;
х= 20 (см)
Значит, АВ=ВС= 20 см, АС= х+4= 20+4= 24 см.
ответ: 20 см, 20 см, 24 см.
Рисунок фактически здесь вообще не нужен, однако, если Вам так легче это представить...
Итак, что мы имеем: треугольник АВС, где угол А=90 градусов, и высота АD делит его на два прямоугольных треугольника.
Начнем с того, что попроще: треугольник ADB (угол D=90 градусов) , катет AD=12, гипотенуза АВ=20, по теореме Пифагора 20^2=12^2+DB^2
Таким образом, сторона DB=16
Теперь рассмотрим второй треугольник, получившийся при делении большого треугольника высотой:
CDA, где угол D =90 градусов.
Катет AD=12, катет DC=X, гипотенуза AC=Y
По все той же теореме Пифагора получаем:
Y^2=12^2+X^2
Теперь рассмотрим исходный треугольник АВС
Катет АВ=20, катет АС=Y (смотри выше) , гипотенуза СВ=X+16
По теореме Пифагора получаем:
20^2+Y^2=(X+16)^2 => Y^2=X^2+32X+256-400 => Y^2=X^2+32X-144
подставляем в уравнение Y^2=12^2+X^2 выраженное значение Y, получаем:
X^2+32X-144=12^2+X^2
32X=288
X=9
Таким образом, гипотенуза ВС=16+9=25
Катет АС=15
Косинус угла С равен отношению прилежащего катета к гипотенузе, т. е. cos C= AC/CB=15/25=3/5