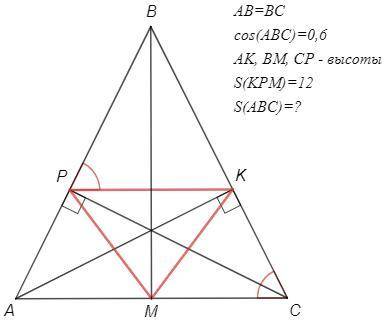
cos(ABC)>0 => △ABC - остроугольный
Отрезок AC виден из точек P и K под прямым углом
=> APKC - вписанный => ∠BPK=∠BCA => PK антипараллельна AC
Аналогично KM и MP.
(Доказали: стороны остроугольного треугольника антипараллельны сторонам ортотреугольника.)
=> △ABC~△KBP~△AMP~△KMC
cos(ABC) =BP/BC =6/10 =3/5
BP=3x, BC=5x, AP=2x
CP=√(BC^2-BP^2)=4x
AC=√(AP^2+CP^2)=√(4+16)x =2√5x
BM - высота и медиана, AM=AC/2=√5x
Площади подобных фигур относятся как квадрат коэффициента подобия.
S(KBP)/S(ABC) =(BP/AB)^2 =(3/5)^2 =9/25
S(AMP)/S(ABC) =(AM/AB)^2 =(√5/5)^2 =5/25
Понятно, что △AMP=△KMC
S(KMP) =S(ABC)-S(KBP)-2(AMP) =(25-9-10)/25 S(ABC) =6/25 S(ABC) =12
=> S(ABC) =12*25/6 =50
Объяснение:
1. Дано: Окр. О,r;
∠1 = ∠2;
Доказать: ∠ОСВ = ∠ОАВ.
Доказательство:
Рассмотрим ΔСОВ и ΔВОА
ОС = ОВ = ОА = r (радиусы одной окружности)
∠1 = ∠2 (по условию)
⇒ ΔСОВ = ΔВОА (по двум сторонам и углу между ними, 1 признак)
В равных треугольниках против равных сторон лежат равные углы.⇒ ∠ОСВ = ∠ОАВ
2. Дано: Окр. О,r;
АВ = ВС - хорды;
Доказать: ∠1 = ∠2.
Доказательство:
Соединим точки А и В с центорм окружности.
Рассмотрим ΔАВО и ΔОВС
АВ = ВС (по условию)
ОВ - общая
АО = ОС = r (радиусы одной окружности)
⇒ ΔАВО = ΔОВС (по трем сторонам, 3 признак)
В равных треугольниках против равных сторон лежат равные углы.⇒ ∠1 = ∠2

В основании пирамиды лежит квадрат. Из вершины пирамиды опустим высоту пирамиды. Основание высоты лежит на пересечении диагоналей квадрата. Проведем сечение через боковое ребро и диагональ основания. это сечение пройдет через противоположное ребро.. Образовался треугольник у которого боковые стороны -боковые ребра пирамиды, а основание диагональ квадрата. Боковые стороны наклонены под углом 60°. Следовательно угол при вершине треугольника 60°. Треугольник равносторонний. Значит диагональ квадрата равна 12 см. Вычислим сторону квадрата основания:
12²= a²+a²=2a²
a²= 12²/2
a=√12²/2=12/√2=12·√2/√2·√2=12√2/2=6√2.
Sосн=6√2·6√2=36·2=72(см²).
Так как пирамида правильная площади боковых граней равны.
Sбок.=4·Sбок.гр.
Площадь боковой грани равна половине произведения длин основания и апофемы (апофема -высота боковой грани). Надо вычислить апофему.
Боковая грань- равнобедренный треугольник. В боковой грани опустим высоту (апофему). Основание высоты делит основание треугольника на два равных отрезка. рассмотрим треугольник, состоящий из бокового ребра, половины основания и апофемы. Боковое ребро -гипотенуза.
H²a=L²бок.реб.-(a/2)², a/2=(6√2)/2=3√2cm.
H²a=12²-(3√2)²,
H²a=12·12-9·2=3·4·3·4-9·2=9(4·4-2)=9·14,
Ha=√9·14=3√14 (cm)
Sбок.реб.=(1/2)·6√2·3√14=·9·√(2·14)=9·√(2·2·7)=9·2√7=18√7(cm²).
Sбок.пов=4·18√7=72√7 (cm²).
Sпол.пов.=Sосн.+Sбок.пов.=72cm²+72√7 (cm²)=72(1+√7)(cm²)