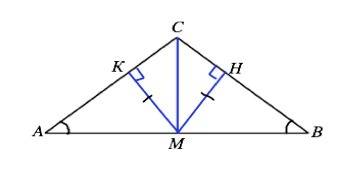
Точка М равноудалена от АС и ВС, т.е. находится на равном от этих сторон расстоянии.
Расстояние от точки до прямой измеряется длиной орезка, проведенного перпендикулярно.
МК⊥АС, МН⊥ВС и КМ=МН
В прямоугольных ∆ АКМ и ∆ ВНМ равны острые углы А = В ( углы при основании равнобедренного треугольника), значит, равна и другая пара острых углов: ∠КМА=∠НМВ.
Катет КМ=катету МН ( по условию)
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.=>
∆ АКМ =∆ ВНМ , следовательно, АМ=ВМ.
∆ АМС = ∆ ВМС по двум сторонам и углу между ними. =>
∠СМА=∠СМВ, они смежные и равны 180°:2=90° .⇒
СМ - проведена из вершины угла треугольника к противоположной стороне, перпендикулярна ей, следовательно, СМ - высота треугольника АВС
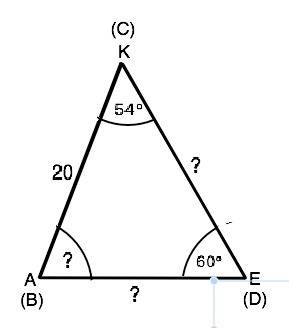
Для начала найдем неизвестные угол и стороны ∆ АКЕ. Сумма углов треугольника 180° => угол КАЕ=180°-(54°+60°=66°
По т.синусов АЕ=АК•sin54°/sin60°. KE=AK•sin66°/sin60°
sin60°=0.8660; sin54°= 0.8090; sin66°=0.9135
AE=20•0,8090/0,8660=18,683≈18,7 см; KE=20•0,9135/0,8660=21,097≈ 21,1 см
Стороны и углы треугольника ВСD имеют те же значения, что и соответствующие углы и стороны ∆ АКЕ, но в условии не указано, какие именно элементы двух треугольников равны. Если в ∆ ВСD сторона ВС=АК, и ∠D=∠Е, то ∠В=∠А=66°,∠С=∠К=54°, ВС=20 см, ВD=AE≈18,7= см, CD=KE≈21,1 см
Две прямые, проведенные из точки S, пересекают три параллельные плоскости
две прямые из точки S тоже образуют плоскость, которая пересекается с заданными ТРЕМЯ плоскостями
так как ТРИ плоскости параллельны , то и линии пересечения плоскостей параллельны
по теореме Фалеса
секущие параллельные прямые
А1В1
А2В2
А3В3
делят стороны угла < A3SB3 на пропорциональные отрезки
Известно, что А1А2=4см, В2В3=9см
обозначим А2А3=В1В2= х
тогда имеем соотношение
A1A2 / A2A3 = B1B2 / B2B3 <подставим сюда цифры
4 / x = x / 9
36= x^2
x= 6
Вычислите А1А3 и В1В3.
A1A3 = A1A2 +A2A3 = 4 +x = 4 +6 =10 см
В1В3 = B1B2 + B2B3 = x + 9 = 6 + 9 =15 см
ОТВЕТ А1А3 = 10 см В1В3 = 15 см