Сумма внешних углов правильного многоугольника всегда равна 360 градусов Сумма внутренних углов = 360 + 720 = 1080 градусов По формуле 180(n-2) = 1080 (n обозначает кол-во сторон првильного многоугольника) находим, что n = 8
длина стороны правильного многоугольника = периметр / кол-во сторон = 144/8 = 18 см
В этом решении n они находят:
По формуле 180(n-2) = 1080
но ведь эта формула, подходит для произвольного многоугольника, а для правильного нужно 180(n-2)/n
но когда я решаю по правильной формуле, ответ не получается 18, почему?? почему используется в решении другая формула?
Рассмотрим прямоугольный треугольник MNP. NH - высота, проведённая к гипотенузе, следовательно, она является средним геометрическим для отрезков MH и HP.
Следовательно :
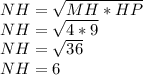
Тогда площадь прямоугольного треугольника MNP равна половине произведения высоты и стороны, к которой проведена эта высота.
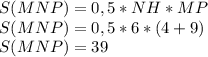
MP - диагональ. Диагональ параллелограмма делит параллелограмм на два равных (в частности и на равновеликих) треугольника. Следовательно, площадь прямоугольника MNPK равна произведению площади треугольника MNP на два.
S(MNPK) = 39*2 = 78.
ответ: 78 (ед^2).
треугольник АВС, уголА=90, ВН-биссектриса,
В=АВ/ВС=3√3/6√3=1/2, что соответствует углу 60, уголАВН=1/2уголВ=60/2=30, ВН=АВ/cosABH=3√3/(√3/2)=6
АС²=ВС²-АВ²=108-27=81, АС=9, АН=х, СН=АС-АН=9-х, АН/СН=АВ/ВС, х/9-х=3√3/6√3, х=3=АН, треугольник АВН прямоугольный, ВН=2*АН=2*3=6 (катет лежит против угла30)
ВН=(2*АВ*ВС*cos (B/2)) / (АС+ВС)=(2*3√3*6√3*(√3/2)) / (3√3+6√3)=6