
Фразу " Равный ему треугольник пересекается с ним только по гипотенузе." нельзя считать точным условием. Поэтому это не задача, а ловушка в духе передачи "Что-Где-Когда". Такие задачи на экзаменах дают тем, кого надо обязательно завалить.
Ну вот, а теперь можно и решить, ровно в том же духе, в каком дано условие.
Итак.
Максимальное количество сторон у фигуры, ограниченной двумя парами катетов - 4. Существует только одна фигура, удовлетворяющая условию - у которой два противоположных угла прямые, и в которую можно вписать окружность - это фигура, состоящая из двух равных прямоугольных треугольников (НЕ СОВПАДАЮЩИХ с заданным), симметрично расположеных относительно общей гипотенузы, (тут есть засада - окружность может касаться и 3 сторон, а не всех 4. Нигде не сказано, что маскимально возможное число сторон, которых касается окружность, равно числу сторон фигуры.).
Загадочное условие "Равный ему треугольник пересекается с ним только по гипотенузе" также может означать только то, что гипотенузы принадлежат одной прямой, или имеют хотя бы одну общую точку, например, в вершине, поскольку в противном случае одна из вершин одного треугольника обязательно лежит внутри другого, и пересечение происходит не по одной, а по двум сторонам (на самом деле тут есть засада - гипотенуза второго треугольника может пересекать первый по двум сторонам - или наоборот).
Таким образом, в предположении, что число сторон, которых касается окружность равно 4, и ОБА треугольника имеют в качестве общих точек только точки на гипотенузах, что нужно найти радиус окружности, вписанной в симметричную относительно диагонали фигуру - четырехугольник, центр которой лежит на диагонали четырехугольника, а сама окружность касается всех сторон.
Важное условие - чтобы точки касания принадлежали катетам.
До этого места все рассуждения более-менее точны. Дальше может быть раздвоение в ИНТЕРПРЕТАЦИИ условия.
1. Первоначально я рассматривал фигуру, составленную из исходного треугольника и его зеркального отражения относительно гипотенузы, и искал радиус вписанной в него окружности.
Центр такой окружности равноудален от катетов, то есть надо найти расстояние от основния биссектрисы прямого угла (то есть от точки пересечения биссектрисы и гипотенузы) до любого из катетов.
Гипотенуза равна 5*2 = 10, откуда катеты треугольника равны 5 и 5√3,
перпендикуляр из основания биссектрисы на катет (любой, например, на катет длины 5) отсекает от треугольника подобный ему треугольник с катетами r, и 5 - r, откуда
(5 - r)/r = 5/5√3 = 1/√3,
откуда r = 5*(3 - √3)/2;
Величину радиуса вписанной в эту фигуру окружности можно сосчитать еще и так - полупериметр фигуры равен p = 5*(1 + √3), а площадь S = 5*5√3, откуда r = 5√3/(1 + √3) = 5*(3 - √3)/2;
2. Есть другая возможность, НЕ противоречащая условию. В этом сучае получается совсем другой ответ.
Предположим, что исходный и равный ему треугольники имеют только одну общую точку - один из концов гипотенуз. Кроме того, предположим, что в фигуру, образовенную катетами и их продолжениями можно вписать окружность (описать то точно можно :))
И потребуем, чтобы ВСЕ 4 точки касания обязательно лежали на катетах. Поскольку между катетами прямой угол, касательные и радиусы, проведенные в точки касания образуют квадрат, и максимально возможный радиус окружности просто равен меньшему из катетов r =5.
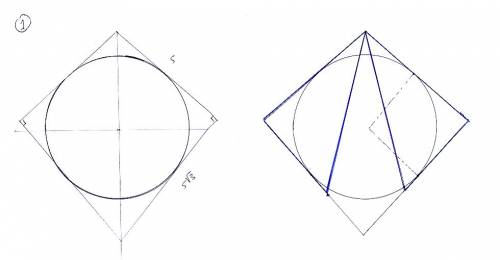
Причем не зависимо от того, какой из концов гипотенуз является общим. На вложенном файле на первом рисунке приведен случай общей гипотенузы, а на втором - когда общей является вершина меньшего угла треугольников. При этом наибольший возможный угол между гипотенузами определяется из условия, что точка касания не выходит за пределы меньшего катета. при этом радиус просто равен этому меньшему катету.
Если же общей является вершина большего угла (между гипотенузой и меньшим катетом), то наибольший возможный угол между гипотенузами равен 60 градусам, при этом большие катеты параллельны, а меньшие лежат на одной прямой (образуют угол в 180 градусов). При этом r = 5. Не стоит удивляться - при этом получается незамкнутая фигура типа "стакан", и две точки касания сливаются в одну, но окружность попрежнему касается всех 4 сторон.
Если потребовать касание только 3 сторон, ответ будет в этом случае тот же r = 5, а вот если окружность касается только 2 сторон четырехугольника (или даже 1), максимально возможное значение r может быть вообще каким угодно (нигде не сказано, что окружность НЕ МОЖЕТ пересекать другие катеты)
С моей точки зрения, за подобные условия учителей надо лишать права заниматься педагогической деятельностью. Пусть идут на телевидение, или в наперстки играют на улицах.
*) вот чем мне решения Гоши68 нравятся - все в них правильно, но я полчаса потратил на выведение этой формулы. Интересно, сколько времени понадобится школьнику :) (я думаю, больше, чем полчаса, даже если он знает, как это делается, и бесконечное время, если не знает).
Треугольник АВС, a = 12, b = 15, c = 18; больший угол конечно - С (напротив стороны с).
Если L - биссектриса угла С, то она делит треугольник на два, площади которых
S1 = (1/2)*a*L*sin(C/2); S2 = (1/2)*b*L*sin(C/2);
Общая площадь S = S1 + S2 = S1 = (1/2)*a*b*sin(C);
откуда
(a + b)*L*sin(C/2) = a*b*sin(C) = 2*a*b*sin(C/2)*cos(C/2);
L = 2*a*b*cos(C/2)/(a + b); (это одна из известных формул длины биссектрисы, я привел её вывод).
С другой стороны, если обозначить cos(C) = х, то из теоремы косинусов
a^2 + b^2 - 2*a*b*x = c^2;
x = (a^2 + b^2 - c^2)/(2*a*b);
Если подставить значения a = 12, b = 15, c = 18; то x = 1/8;
Из тригонометрической формулы 2*(cos(C/2))^2 - 1 = cos(C);
теперь легко найти косинус половинного угла по значению косинуса всего угла С
cos(C/2) = 3/4;
откуда
L = 2*12*15*3/(4*(12 + 15)) = 10;
Еще один решения, самый очевидный, основан на формуле L^2 = a*b - z*y; где z и y - отрезки, на которые биссектриса делит сторону с.
То есть
z + y = c;
z/y = a/b;
откуда z = c*a/(a + b); y = c*b/(a + b);
Если подставить значения a = 12, b = 15, c = 18; то z = 18*12/27 = 8; y = 10;
L^2 = 12*15 - 8*10 = 100;
L = 10;
само собой, формулу L^2 = a*b - z*y; надо уметь выводить, что тоже совсем не просто :)
Я не смог удержаться, и решил привести полное доказательство формулы, которую Гоша68 использовал :) Ну просто вот не могу отказать себе...
Из теоремы косинусов
cos(C) = (a^2 + b^2 - c^2)/(2*a*b);
откуда
1 + cos(C) = ((a + b)^2 - c^2)/(2*a*b) = 2*p*(p - c)/(a*b); где p = (a + b + c)/2;
отсюда cos(C/2) = √(p*(p - c)/a*b); осталось подставить это в доказанное ранее выражение L = 2*a*b*cos(C/2)/(a + b); и получится Гошина формула.
Что-то это мне напоминает :)
Чего то я завелся :) А как выводится формула L^2 = a*b - z*y; Это очень простая теорема, но очень красиво доказывается, не могу себе отказать :)
Пусть треугольник АВС, СК - биссектриса, и пусть М - это точка пересечения биссектрисы СК с описанной вокруг АВС окружностью. Тогда угол СВА равен углу СМА - они опираются на одну дугу АС, а углы АСМ и МСВ тоже равны, потому что СМ - биссектриса угла С (в этом вся соль!). Поэтому треугольники АМС и ВКС подобны, то есть
СМ/CA = CD/CK; или (CK + KM)*CK = CA*CB; откуда
CK^2 = CA*CB - C*K*KM;
Но CK*KM = AK*KB; (ну, уж это то вы знаете... хотя это автоматически следует из подобия треугольников АКМ и СКВ...)
откуда CK^2 = CA*CB - KA*KB; чтд.
Ну вот, поскольку я полностью исчерпал тему, любой модератор может смело это удалить, как нарушение (ну в самом деле, нет чертежа, много лишнего текста, полно выходящих за рамки школьной программы формул, в некоторых местах - откровенный флуд..) Удаляйте смело, а я погляжу, кто это сделает :)