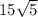 (кв. единица)
(кв. единица)
Объяснение:
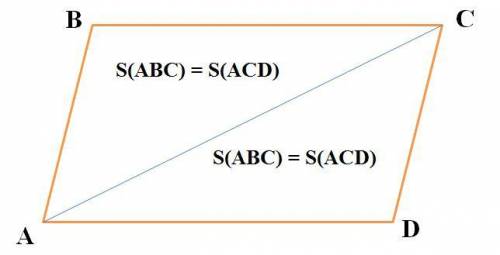
По условию задано координаты трёх его вершин параллелограмма АВСD: А(27;18;20) , В(24;18;16) и С(18;21;18). Так как верно свойство (см. рисунок) "Диагональ параллелограмма делит его на два равных треугольника", то площадь параллелограмма S(ABCD) равна удвоенной площади одного из треугольников, то есть
S(ABCD)=2·S(ABC).
В нашем случае диагональ AC делит параллелограмм на два равных треугольника. Поэтому достаточно найти площадь S(ABC) треугольника ABC по формуле Герона:
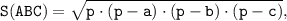
где p - полупериметр: 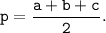
Стороны треугольника ABC находим по формуле расстояния между двумя точками с координатами M(x₁; y₁; z₁) и N(x₂; y₂; z₂):
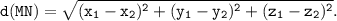
Так как А(27;18;20), В(24;18;16) и С(18;21;18), то
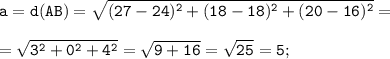
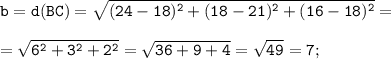
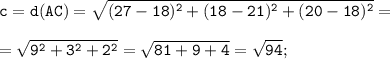
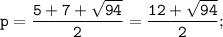
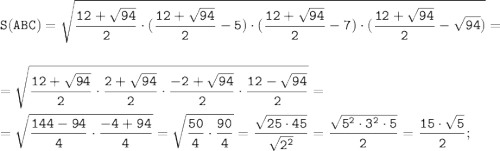
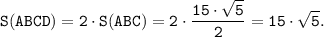
номер 1
M=100
C=60
K=20
т.к в треугольнике против большей стороны лежит больший угол
номер 2
две из сторон треугольника равны т.к дан равнобедренный треугольник
это значит что основание на 15 см меньше любой из боковых сторон
пусть х- одна из боковых сторон
тогда основание это х-15
составим уравнение
2х+х-15=72
3х=72+15
3х=87
х=29
каждая боковая сторона равна 29 см
т.к боковые стороны равны то основание равно 72-(29×2) =14см
ответ: боковые стороны- по 29 см
основание- 14см
Объяснение:
P.s Аластор на аве- здоровья маме
Задача №3. Равнобедренная трапеция с основаниями 10 см и 18 см и высотой 3 см вращается около меньшего основания. Найдите площадь поверхности тела вращения.
===========
При вращении данной трапеции получится цилиндр с «вставленными» внутрь него с обеих концов равными конусами
Пусть дана трапеция АВСD, AB=CD.
АD - высота цилиндра; высота трапеции ВН - радиус тела вращения, АВ=СD - образующие конусов.
Высоты трапеции, опущенные из вершин тупых углов, «отсекают» от нее два равных прямоугольных треугольника АВН и СDК. АН=DK=(AD-BC):2=4 =>
Из ∆ АВН по т.Пифагора АВ=5. (это так называемый "египетский" треугольник.
Искомая площадь равна сумме боковой поверхности цилиндра и боковой поверхности двух равных конусов.
S=2πrH+2•πrL=2π•r•(H+L)
S=6π•(18+5)=6π•23=138 π см² или ≈ 433,5 см²
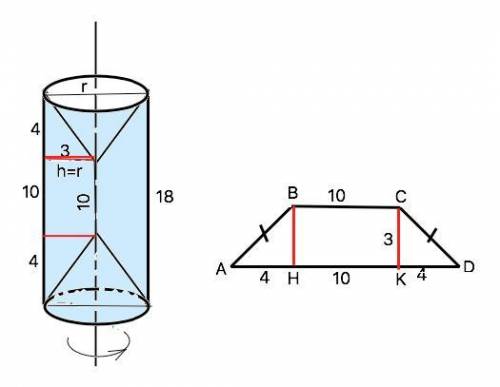
решение представлено на фото
Объяснение: