Дано:
Р=50 см
АС - диагональ и высота параллелограмма АВСD.
пусть АВ=DC=х,
тогда AD=ВС=(х+1).
Р = 2*х+2*(х+1) = 4*х+2 = 50,
х = (50-2)/4 = 12.
АВ=DC=12 (см), а AD=ВС=(12+1)=13 (см).
АD - гипотенуза прямоугольного треугольника ADC
AD^2 = АС^2+DC^2(по теореме Пифагора)
13^2 = АС^2+12^2
АС^2 = 13^2-12^2
АС = корень из (13^2-12^2) = корень из (169-144) = корень из (25) = 5 (см)
ответ: 5 см.
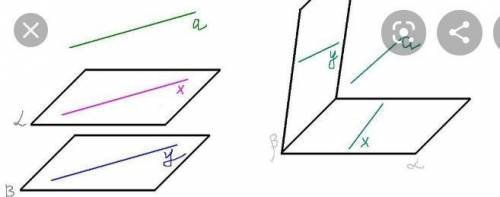
А) нет, т. к. если одна из параллельных прямых пересекает плоскость, то и вторая прямая пересечёт эту плоскость.
б) могут.
Пусть в плоскости ą лежит прямая с||а, b пересекает плоскость ą в точке, принадлежащей прямой с. Тогда, если прямая пересекает одну из двух параллельных прямых, то она пересечёт и вторую.
в) могут. Т. к. а||плоскости альфа, то существует плоскость ß, в которой лежит а. если одна из 2 прямых лежит в некоторой плоскости (в данном случае прямая а), а другая прямая (прямая b) пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Задача 1 - ответ: 7 см².
Задача 2 - ответ: 37,5 см².
Объяснение:
Задача 1.
Площадь треугольника равна половине произведения сторон треугольника на синус угла между ними:
S = (4*7*sin30°) :2 = (28*0,5) : 2 = 7 см².
ответ: 7 см².
Задача 2.
Сумма углов ромба, прилегающих к одной его стороне, равна 180°. Поэтому если один угол равен 150°, то второй угол равен 30°.
Так как ромб состоит из двух равновеликих треугольников, то его площадь можно выразить как удвоенное произведение площади одного треугольника, равную половине произведения двух сторон ромба на синус угла между ними:
S = [(5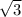 * 5
* 5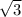 *sin30°) :2] * 2 = 5
*sin30°) :2] * 2 = 5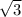 * 5
* 5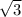 *sin30° = 25*3*0,5 = 37,5 см².
*sin30° = 25*3*0,5 = 37,5 см².
ответ: 37,5 см².
АС - диагональ и высота параллелограмма АВСD.
пусть АВ=DC=х,
тогда AD=ВС=(х+1).
Р = 2*х+2*(х+1) = 4*х+2 = 50,
х = (50-2)/4 = 12.
значит, АВ=DC=12 (см), а AD=ВС=(12+1)=13 (см).
АD - гипотенуза прямоугольного треугольника ADC, значит, по теореме Пифагора,
AD^2 = АС^2+DC^2
13^2 = АС^2+12^2
АС^2 = 13^2-12^2
АС = корень из (13^2-12^2) = корень из (169-144) = корень из (25) = 5 (см).
ОТВЕТ: 5 см.