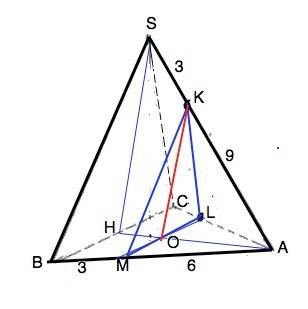
Основание правильной пирамиды - равносторонний треугольник АВС. Вершина S правильной пирамиды проецируется в т.О – центр правильного треугольника АВС.
Сечение KLM- треугольник.
Искомая площадь S=a•h:2, где a=ML, h=KO
Угол МАL=60°, CL=BM, следовательно, AL=AM ⇒∆ AML – правильный.
АL=AM=9-3=6,⇒ ML=6
Высота основания AH=AB•sin60°=9√3/2=4,5√3
Грани пирамиды - равнобедренные треугольники.
По т.Пифагора из ∆ SHB:
SH²=SB²-BH²=144-20,25=123,75
По т. косинусов вычислим косинус ∠SAH:
SH²=SA²+AH² - 2•SA•HA•cos∠SAH
123,75=144+60,75 - 2•12•4,5√3•cosSAH
-81= -12•9√3•cos∠SAH
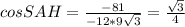
Из ∆ KLM по т. косинусов
КО²=КА²+АО²-2•AO•KO•cos∠KAO
КА=SA-SK=12-3=9
AO=2/3 AH=3√3
КО²=81+27 - 2•9•3√3•√3):4
КО²=67,5
КО=1,5√30
S ∆KLM=0.5•6•1,5√30=4,5√30
В равностороннем треугольнике биссектриса является также и высотой и медианой.
Зная это, найдем АД:
АД=АС/2=(14 √3)/2=7√3 (так как ВД – медиана)
Рассмотрим треугольник АВД: угол АДВ= 90 градусов (так как ВД высота)
По теореме Пифагора найдем ВД:
ВД=√АВ^2-AД^2)=((14√3)^2-(7√3)^2)= √(588-147)= √441=21
Второй вариант:
Формула нахождения биссектрисы в равностороннем треугольнике:
L=(a√3)/2 (где L – биссектриса, а сторона треугольника)
L=(14√3*√3)-2=(14*3)/2=42/2=21