Отрезки МК и NP параллельны соседним сторонам прямоугольника, => соответственно равны им, пересекаются под прямым углом и делят АВСD на 4 прямоугольника, (неважно, равной или разной площади). Обозначим точку пересечения МК и NP буквой О.
а)
Стороны четырехугольника МNKP являются диагоналями получившихся прямоугольников и делят каждый из них пополам (свойство). Поэтому площадь MNKP равна сумме площадей этих половин, т.е. равна половине площади ABCD.
б)
Площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними.
Так как S(ABCD)=AB•CD, МК=АD и NP=AB, а sin90°=1, то S(MNKP)=MK•NP•sin90°=0,5•S(ABCD).
в)
S(MNKP)=S∆MNP+S∆NKP=0.5•MO•NP+0.5•KO•NP=0,5•NP•(MO+OK) => S(MNKP)=0,5•NP•MK =>
S(MNKP) =0,5•S(ABCD), т.к. NP=AB и МК=АD

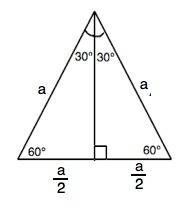
В равностороннем треугольнике все стороны равны между собой, все углы равны 60°. а биссектриса является и медианой и высотой. Поэтому она делит такой треугольник на два равных прямоугольных.
Примем сторону треугольника равной а. Тогда высота - один катет, половина стороны - другой катет, сторона - гипотенуза.
По т.Пифагора а²=(a/2)²+h²
откуда а²=4h²/3
Заменив в этом выражение h на 12√3, получим
а²=4•12*•3/3=4•12², откуда
а=√(4•12*)=2•12=24 (ед. длины)
-----------------
Короткое решение:
Биссектриса (медиана, высота) равностороннего треугольника h=а•sin60°, откуда
a=h:sin60°
a=12√3:(√3/2)=24
AB²=BF²+AF²
AB²=576+324
AB²=900
AB=30