Этот угол можно найти двумя
а) геометрическим,
б) векторным.
а) При этом делаем перенос отрезка ВМ в общую точку с отрезком В1С, а именно точкой В в точку С и это будет общая точка С.
Получаем треугольник В1СМ. Находим длины его сторон.
В1С = √(9 + 25) = √34,
СМ = √(4² + (3/2)² + (5/2)²) = √(16 + 2,25 + 6,25) = √24,5.
В1М = √(4² + (3+(3/2))² + (5/2)²) = √(16 + 20,25 + 6,25) = √42,5 .
Угол С (общая точка двух отрезков) находим по теореме косинусов.
cos С = ((B1C)² + CM² - (B1M)²)/(2*{B1C|*|CM|).
Подставив значения, получаем cos C = 0,277184.
Угол С равен 1,289935 радиан или 73,907817 градуса.
б) Поместим параллелепипед точкой В в начало координат, АВ по оси Ох, ВС - по оси Оу.
Координаты точек:
В1(0; 0; 5), С(0; 3; 0), вектор В1С(0; 3; -5), модуль √34.
В(0; 0; 0), М(4; 1,5; 2,5), вектор ВМ(4; 1,5; 2,5, модуль √24,5.
cos C = |(0 + 4.5 + (-12.5)|/(√34*√24.5) = 0,277184.
Угол равен 1,289935 радиан или 73,907817 градуса.
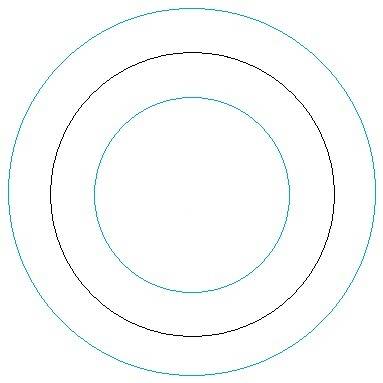
1) Пусть точка M лежит вне окружности. O - центр окружности, точка T - пересечение отрезка OM и окружности. Возьмем на окружности точку T1, не лежащую на OM. В треугольнике MT1O сторона OM меньше суммы двух других сторон (неравенство треугольника),
MT+OT<MT1+OT1 <=> MT<MT1 (OT=OT1, радиусы)
Таким образом, чтобы длина MT была минимальной, T должна лежать на OM. Если M вне окружности, MT=1, OT=2000, то OM=MT+OT=2001. Искомое ГМТ - окружность радиусом 2001 с центром данной окружности.
2) Аналогично доказывается, что если точка M лежит внутри окружности, то искомое ГМТ - окружность радиусом 1999 (OM=OT-MT) с центром данной окружности.

1 час 24 мин = 84 мин
пусть бак Х литров
скорость первого насоса Х/12
скорость второго насоса Х/14
скорость третьего насоса Х/84
общая скорость Х/12+Х/14+Х/84= (7Х+6Х+Х )/84 = Х/6
время для трех насосов t = X / (X/6) = 6 мин
ОТВЕТ 6 мин