Внимание : тут два варианта .
96 или 78 см
Чертёж в приложении.
Объяснение:
Вариант 1 (если бисс АК)
1) уг 1=уг 2 (как накрест лежащие при парал прямых);
уг 1=уг 3 (тк бисс);
тогда уг 2=уг3 => треуг АВК–равнобед =>АВ=ВК=19 и =СD (как стороны парал);
2) ВС=19+10=29=АD;
3) Р =(19+29)*2=96 см
Вариант 2 (если бисс DК)
1) уг 1=уг 2 (как накрест лежащие при парал прямых);
уг 1=уг 3 (тк бисс);
тогда уг 2=уг3 => треуг DСК–равнобед =>DС=СК=10 и =АВ (как стороны парал);
2) ВС=19+10=29=АD;
3) Р =( 10+29)*2=78
Если что-то непонятно , пишите в комментах.
Успехов в учёбе! justDavid
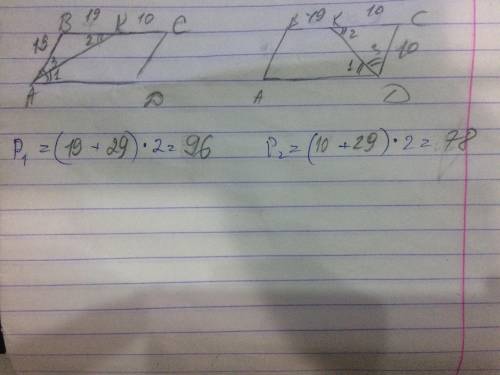
Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство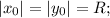
учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти) 
уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2
;
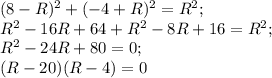R=20 или R=4
значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат
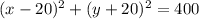
и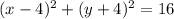 
вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр
Ищем координаты середины отрезка АВ,
(0;2)
ищем уравнение пряммой АВ в виде y=kx+b
3=-2k+b;
1=2k+b;
2=-4k
1=2k+b;
k=-0.5
b=2;
y=-0.5x+2
перпендикулярные пряммые связаны соотношением угловых коэффициентов
k_1k_2=-1
поєтому угловой коєффициент искомой пряммой равен k=-1/(-0.5)=2
учитывая что искомая пряммая проходит через точку С ищем ее уравнение в виде
y=kx+b (k=2)
2=2*0+b;
b=2
y=2x+2 или y-2x-2=0
в чем ошибка у вас - неведомо, ибо вы своего решения не предоставили
AC=CB ⇒
AB² = 2AC²
8 = 2AC²
AC = 2 ⇒ CB = 2
2.
Если угол А = 30°, то угол В - 60°
И по теореме синусов:
Th sin:
CB/sin 30° = AC/sin 60°
СВ = 1/2 * 3√3 * 2/√3 = 3
3.
√243 = 9√3
Все также, как и во второй:
CB/sin 30° = AC/sin 60°
CB = 1/2 * 9√3 * 2/√3 = 9
4.
√32 = 4√2
AB² = AC²+CB²
AC=CB ⇒
AB²=2AC²
32=2AC²
AC=4
CB=4
5.
√128=8√2
AB²=2AC²
128=2AC²2
AC=8
CB=8
6.
(см. третью задачу, то же самое)
Остальные решить не могу, данных о гипотенузе не хватает. Напишите - решу. Удачи