Объяснение:
10)
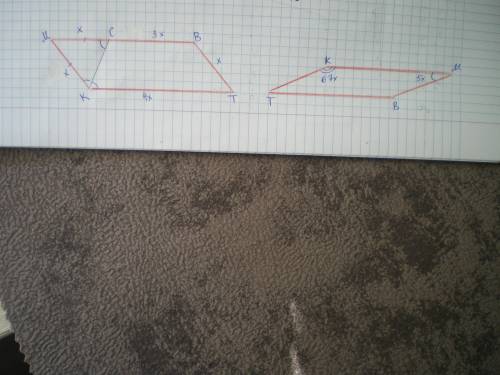
Дано: КМВТ - параллелограмм, Р=65 см, КС - биссектриса, МС/ВС=1/3.
Найти МВ.
∠МКС=∠СКТ по определению биссектрисы
∠СКТ=∠МСК как внутренние накрест лежащие при МВ║КТ и секущей КС
значит, ΔМКС - равнобедренный и МК=МС.
Пусть МС=МК=ВТ=х см, тогда ВС=3х см, КТ=МВ=х+3х=4х см.
Составим уравнение: х+х+4х+4х=65
10х=65; х=6,5
МВ=КТ=6,5 * 4 = 26 см.
ответ: 26 см.
11)
Дано: КМВТ - параллелограмм ∠М/∠К=5/67. Найти ∠К.
Сумма углов параллелограмма, прилегающих к одной стороне, составляет 180°.
Пусть ∠5х°, тогда ∠К=67х°.
Составим уравнение:
5х+67х=180; 72х=180; х=2,5
∠К=67*2,5=167,5°
ответ: 167,5°
Пусть даны два прямоугольных треугольника ABC и DEF, стороны прямоугольного треугольника ABC равны 6, 8 и 10 см, угол А=30 градусов, гипотенуза DF треугольника DEF равна 10 см и угол D=30 градусов. Найти катеты треугольника DEFПусть даны два прямоугольных треугольника ABC и DEF, стороны прямоугольного треугольника ABC равны 6, 8 и 10 см, угол А=30 градусов, гипотенуза DF треугольника DEF равна 10 см и угол D=30 градусов. Найти катеты треугольника DEFПусть даны два прямоугольных треугольника ABC и DEF, стороны прямоугольного треугольника ABC равны 6, 8 и 10 см, угол А=30 градусов, гипотенуза DF треугольника DEF равна 10 см и угол D=30 градусов. Найти катеты треугольника DEFПусть даны два прямоугольных треугольника ABC и DEF, стороны прямоугольного треугольника ABC равны 6, 8 и 10 см, угол А=30 градусов, гипотенуза DF треугольника DEF равна 10 см и угол D=30 градусов. Найти катеты треугольника DEF
Это легко проверить: разбейте шестиугольник на 4 треугольника из любого одного угла (сумма углов треугольника всегда равна 180 градусам), то есть умножьте 180 на 4, а после этого разделите на количество углов (их у нас 6).
180*4=720;
720/6=120.
Есть ещё один разделите правильный шестиугольник диагоналями.
У вас получились 6 равносторонних треугольников, каков угол равностороннего треугольника? 60 градусов.
В каждом углу шестиугольника оказываются два треугольника. Если сложить их углы, то у нас опять же получится 120 градусов.