Объяснение:
Задача имеет 2 решения.
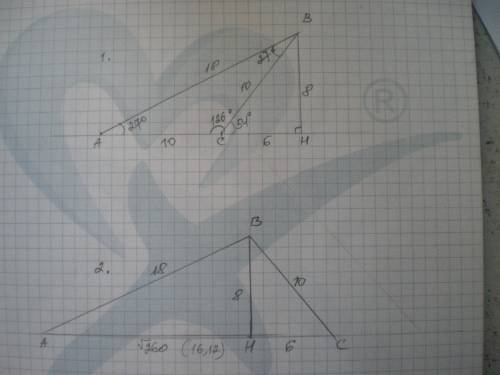
1. Наклонные проведены по одну сторону от перпендикуляра.
Имеем прямую АН, ВН⊥АН, ВН=8 см, ВС=10 см, АВ=18 см. Найти АС.
ΔВСН - прямоугольный, ВН=8 см, ВС=10 см, тогда СН=6 см (египетский треугольник).
По теореме синусов sin∠ВСН=8\10, ∠ВСН=54°.
∠АСВ=180-54=126°.
Найдем ∠А из ΔАВС.
sin126\АВ=sinА\ВС; sinА=0,809*10:18=0,4494; ∠А=27°
∠АВС=180-126-27=27°, значит,ΔАВС - равнобедренный и АС=ВС=10 см. ответ 10 см.
2. Наклонные проведены по обе стороны от перпендикуляра.
Дано: АС⊥ВН; ВН=8 см, АВ=18 см, ВС=10 см. Найти АС.
В ΔВСН СН=6 см (египетский треугольник), АН найдем по теореме Пифагора:
АН=√(АВ²-ВН²)=√(324-64)=√260≈16,12 см.
АС=16,12 + 6 = 22,12 см.
ответ: 22,12 см.
1. AB=(0-(-5); 7-(-2); -2-1), т.е их координат точки В вычитаем поочередно координаты точки А
получаем АВ(5;9;-3)
DA=(4-(-5);-2-(-2);-2-1)
DA=(9;0;-3)
со след. векторами аналогично
2. DA=(9;0;-3)
Для того, чтобы разложить по координатным векторам вектор DA мы возводим в квадрат его координаты, складываем
и берем их под корень. т.е.:
/DA/=√81+0+9=√90≈9,5
DA=9i+0j-3k
3.СВ+DА=складываешь координаты, которые найдены в 1 пункте
и т.д.
5.Координаты середины отрезка равны полусумме соответствующих координат концов отрезка. т.е. координаты отрезка ВС делишь на 2.
Карамель(думать о чём?) о карамели.
Тоннель(думать о чём?) о тоннели.
Хоть эти слова существительные, но разного рода, поэтому и окончания будут разные, даже в одинаковом падеже.